GAMES101 Lecture Notes
GAMES101现代计算机图形学入门课程笔记
我的作业实现:My homework implementation
线性代数
叉乘
叉乘对于右手系来说使用右手螺旋定则。
笛卡尔坐标系下:
$$ \vec{a} \times \vec{b} = \begin{pmatrix} y_az_b-y_bz_a \cr z_ax_b - z_bx_a \cr x_ay_b - y_ax_b \end{pmatrix} $$
矩阵写法:
$$ \vec{a} \times \vec{b} = A * b = \begin{pmatrix}0 & -z_a & y_a \cr z_a & 0 & -x_a \cr -y_a & x_a & 0\end{pmatrix} $$
$A$叫做$\vec{a}$的伴随矩阵
变换
齐次坐标
齐次坐标引入是为了线性表示仿射变换(线性变换+平移变换)
2D点的表示:$(x, y, 1)^T$
2D向量的表示:$(x, y, 0)^T$
2D变换
缩放 $$ \textbf{S}(s_x, s_y) = \begin{pmatrix}s_x & 0 & 0 \cr 0 & s_y & 0 \cr 0 & 0 & 1\end{pmatrix} $$
旋转
注意$\alpha$为正表示逆时针 $$ \textbf{R}(\alpha) = \begin{pmatrix}\cos\alpha & -\sin\alpha & 0 \cr \sin\alpha & \cos\alpha & 0 \cr 0 & 0 & 1 \end{pmatrix} $$
平移 $$ \textbf{T}(t_x, t_y) = \begin{pmatrix}1 & 0 & t_x \cr 0 & 1 & t_y \cr 0 & 0 & 1\end{pmatrix} $$
3D变换
变换矩阵
$$ \begin{pmatrix}x’ \cr y’ \cr z’\end{pmatrix} = \begin{pmatrix}a & b & c & t_x \cr d & e & f & t_y \cr g & h & i & t_z \cr 0 & 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}x \cr y \cr z\end{pmatrix} $$
先应用线性变换再应用平移
正交矩阵
Transform matrix $\textbf{T}$是正交矩阵,则
$$ \textbf{T}^{-1} = \textbf{T}^T $$
3D旋转变换
旋转变换矩阵
绕x轴旋转 $$ \mathbf{R}_x(\alpha)=\left(\begin{array}{cccc} 1 & 0 & 0 & 0 \cr 0 & \cos \alpha & -\sin \alpha & 0 \cr 0 & \sin \alpha & \cos \alpha & 0 \cr 0 & 0 & 0 & 1 \end{array}\right) $$
绕y轴旋转 $$ \mathbf{R}_y(\alpha)=\left(\begin{array}{cccc} \cos \alpha & 0 & \sin \alpha & 0 \cr 0 & 1 & 0 & 0 \cr -\sin \alpha & 0 & \cos \alpha & 0 \cr 0 & 0 & 0 & 1 \end{array}\right) $$
绕z轴旋转 $$ \mathbf{R}_z(\alpha)=\left(\begin{array}{cccc} \cos \alpha & -\sin \alpha & 0 & 0 \cr \sin \alpha & \cos \alpha & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \end{array}\right) $$
欧拉角 $$ \textbf{R}_{xyz}(\alpha, \beta, \gamma) = \textbf{R}_x(\alpha)\textbf{R}_y(\beta)\textbf{R}_z(\gamma) $$
Rodigues旋转公式
绕着任意一个轴$\textbf{n}$旋转$\alpha$角度的变换为
$$ \textbf{R}(n, \alpha) = \cos(\alpha)\textbf{I} + (1 - \cos(\alpha))\textbf{n}\textbf{n}^T + \sin(\alpha)\underbrace{\begin{pmatrix}0 & -n_z & n_y \cr n_z & 0 & -n_x \cr -n_y & n_x & 0\end{pmatrix}}_{\textbf{N}, \text{dual matrix of n}} $$
视角变换(View Transform)
视角变换,包括View/camera transform和projection transform,与model transform合称MVP变换。
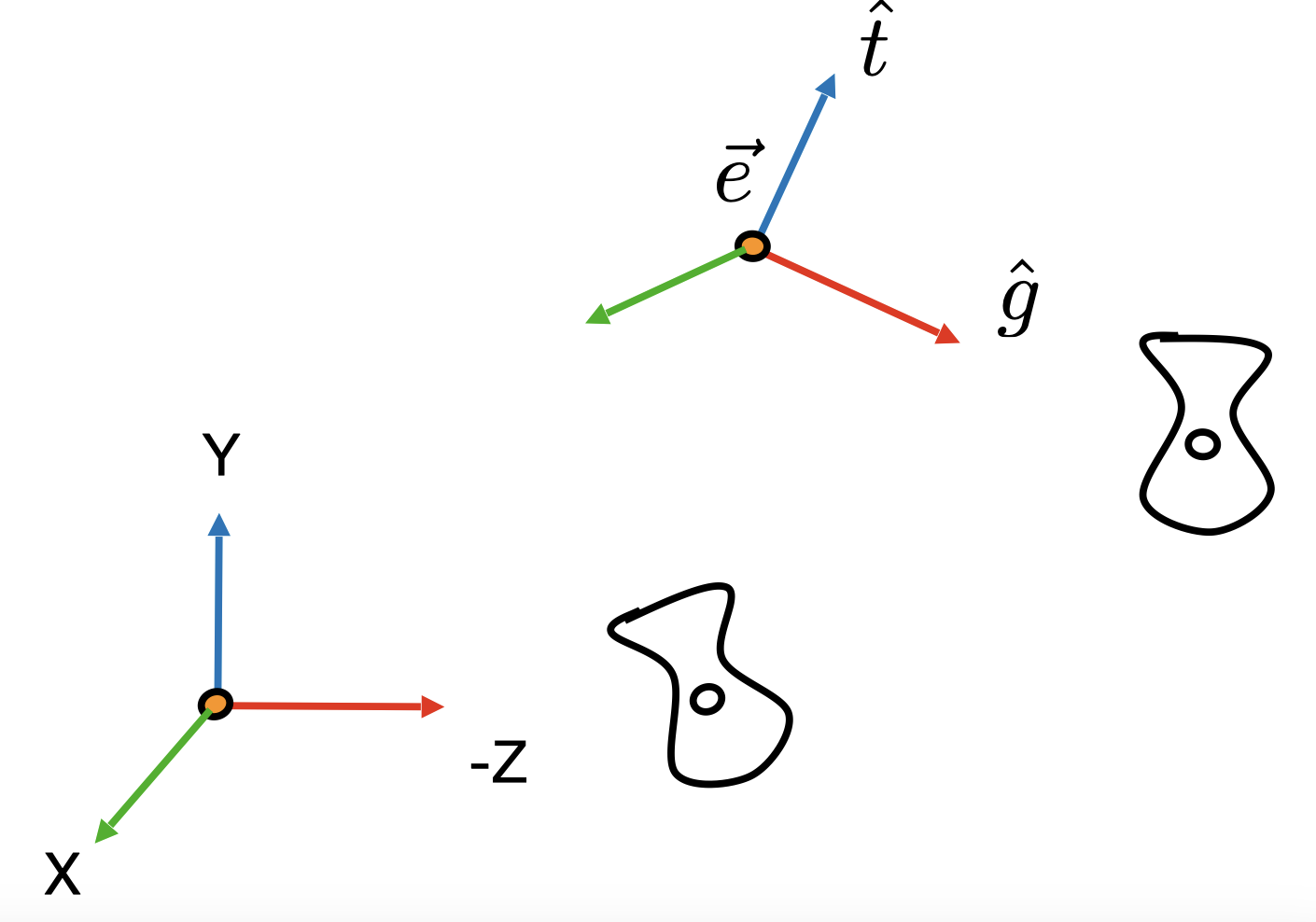 默认情况下相机朝向-z轴, y轴朝上。我们需要将$\vec{e}$首先平移到圆点,然后将$\hat{g}$指向-z,$\hat{t}$指向y轴,$\hat{g}\times\hat{t}$指向x轴。
默认情况下相机朝向-z轴, y轴朝上。我们需要将$\vec{e}$首先平移到圆点,然后将$\hat{g}$指向-z,$\hat{t}$指向y轴,$\hat{g}\times\hat{t}$指向x轴。
考虑逆变换,即x轴正方向旋转至$\hat{g}\times\hat{t}$,y轴正方向旋转至$\hat{t}$,z轴负方向旋转至$\hat{g}$。我们可以轻易得到该变换的旋转矩阵为
$$ R_{view}^{-1} = \begin{bmatrix}x_{\hat{g}\times\hat{t}} & x_{t} & x_{-g} & 0 \cr y_{\hat{g} \times \hat{t}} & y_t & y_{-g} & 0 \cr z_{\hat{g} \times \hat{t}} & z_t & z_{-g} & 0 \cr 0 & 0 & 0 & 1\end{bmatrix} $$
因此原本的旋转矩阵应该为该矩阵的逆,由于旋转矩阵是正交阵,因此转置即可。
$$ R_{view} = \begin{bmatrix}x_{\hat{g}\times\hat{t}} & y_{\hat{g} \times \hat{t}} & z_{\hat{g} \times \hat{t}} & 0 \cr x_{t} & y_t & z_t & 0 \cr x_{-g} & y_{-g} & z_{-g} & 0 \cr 0 & 0 & 0 & 1\end{bmatrix} $$
投影变换(Project Transform)
正交投影(Orthographic Projection)
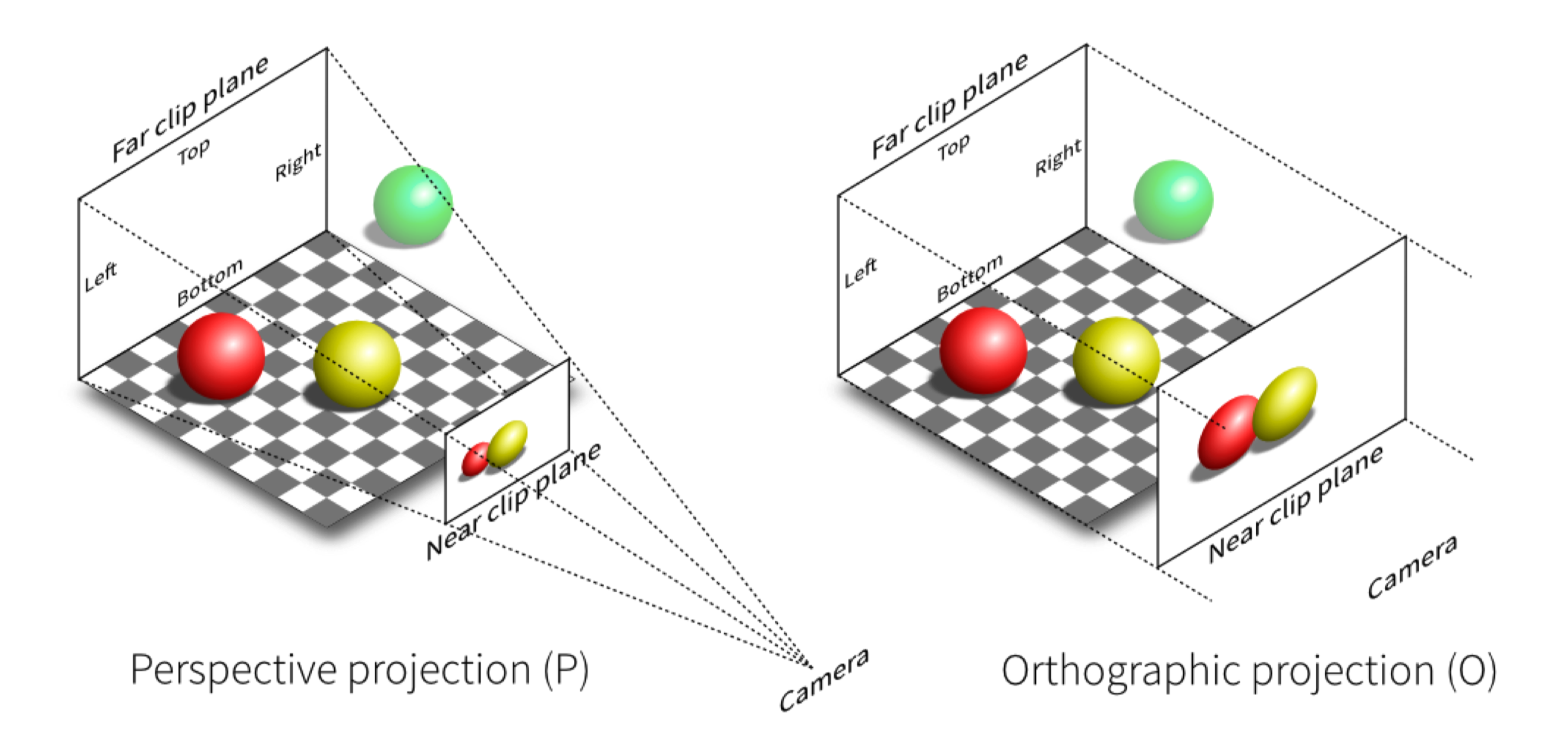
正交投影没有近大远小的效果。直接将$[l, r] \times [b, t] \times [f, n]$的盒式可见空间投影到$[-1, 1]$的标准立方体中。
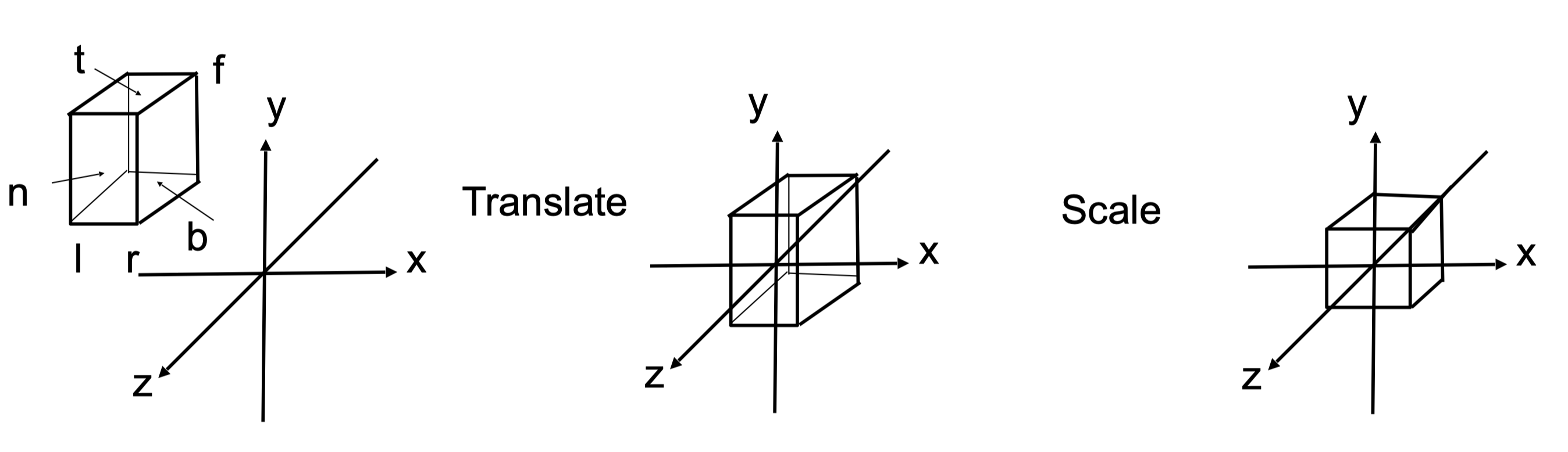
先将立方体中心平移到原点,再进行缩放变换,使得边界为$[-1, 1]$。
$$ M_{\text {ortho }}=\left[\begin{array}{cccc} \frac{2}{r-l} & 0 & 0 & 0 \cr 0 & \frac{2}{t-b} & 0 & 0 \cr 0 & 0 & \frac{2}{n-f} & 0 \cr 0 & 0 & 0 & 1 \end{array}\right]\left[\begin{array}{cccc} 1 & 0 & 0 & -\frac{r+l}{2} \cr 0 & 1 & 0 & -\frac{t+h}{2} \cr 0 & 0 & 1 & -\frac{n+f}{2} \cr 0 & 0 & 0 & 1 \end{array}\right] $$
透视投影
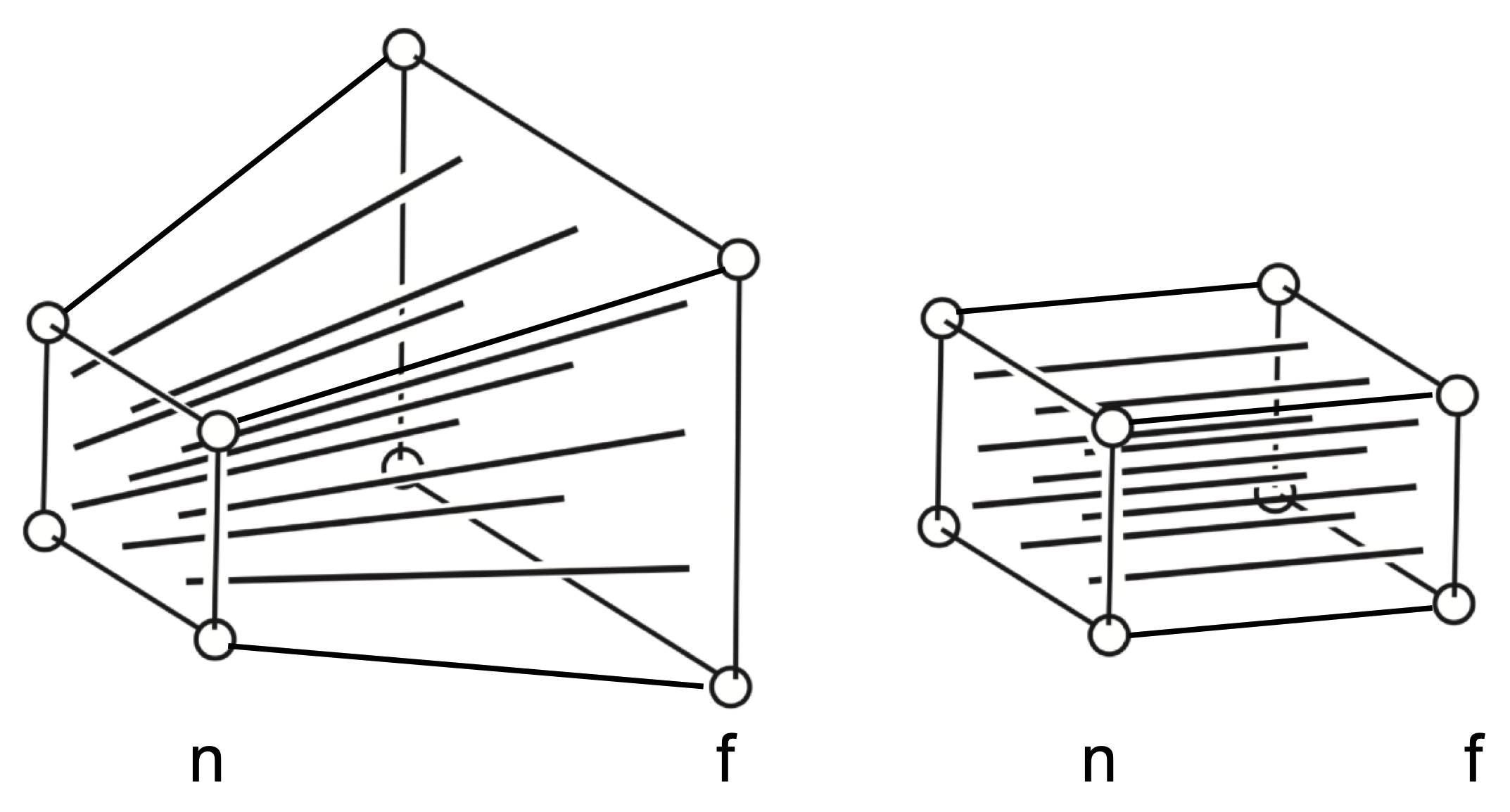
透视投影考虑到了近大远小的效果,模拟人类眼睛看到世界的过程。透视投影的视体(Viewing frustum)类似于一个锥台。我们需要将这个方平截头体“压缩”为一个立方体,然后对这个立方体进行正交投影变换即可。
“压缩”这个锥台是需要保证n面不变,f面映射到和n面相同的大小。
对于n面和f面中间所有的点$(x, y, z)$来说,可以用相似三角形求得$x’$和$y’$的值为$x’=\frac{n}{z}x$, $y’=\frac{n}{z}y$,如下图所示。
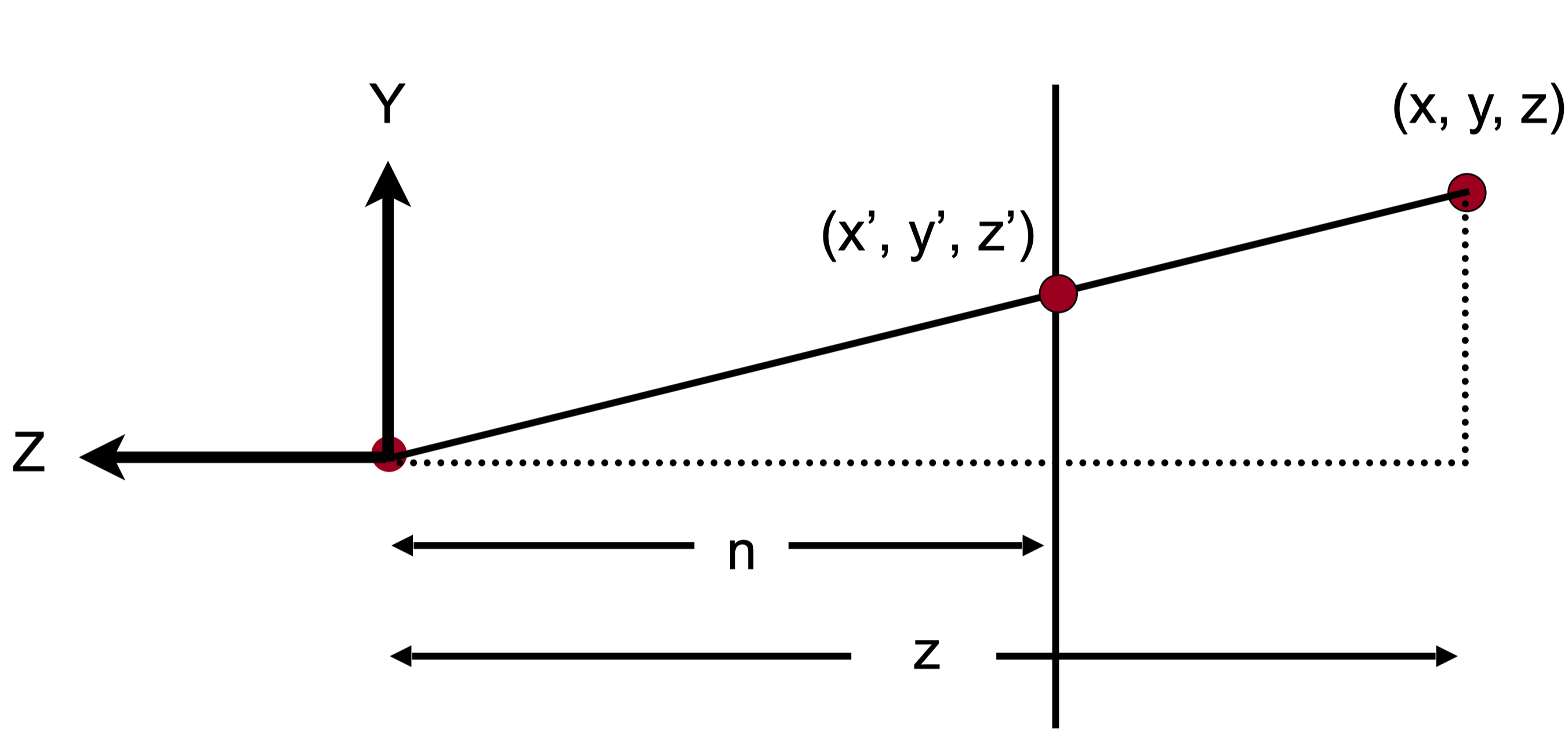
但是要注意,$z’$的大小目前是未知的。
因此我们可以得出以下关系:
$$ M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)}\left(\begin{array}{l} x \cr y \cr z \cr 1 \end{array}\right)=\left(\begin{array}{c} n x \cr n y \cr \text { unknown } \cr z \end{array}\right) $$
$$ M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \cr 0 & n & 0 & 0 \cr ? & ? & ? & ? \cr 0 & 0 & 1 & 0 \end{array}\right) $$
由于当在n平面上所有的点都会保持不变,因此
$$ M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)} \left(\begin{array}{c} x \cr y \cr n \cr 1 \end{array}\right)=\left(\begin{array}{c} n x \cr n y \cr n^2 \cr n \end{array}\right) $$
同时在f平面上,$(0, 0, f)$在变换后应当保持不变,因此
$$ M_{\text {persp } \rightarrow \text { ortho }}^{(4 \times 4)} \left(\begin{array}{c} 0 \cr 0 \cr f \cr 1 \end{array}\right)=\left(\begin{array}{c} 0 \cr 0 \cr f^2 \cr f \end{array}\right) $$
根据这两个性质,可以求解得到
$$ M_{\text {persp } \rightarrow \text { ortho }}=\left(\begin{array}{cccc} n & 0 & 0 & 0 \cr 0 & n & 0 & 0 \cr 0 & 0 & n + f & -nf \cr 0 & 0 & 1 & 0 \end{array}\right) $$
因此最终的透视投影变换为
$$ M_{\text {persp }}=M_{\text {ortho }} M_{\text {persp } \rightarrow \text { ortho }} = \begin{pmatrix}\begin{array}{cccc} \frac{2n}{r-l} & 0 & 0 & -\frac{r-l}{r+l} \cr 0 & \frac{2n}{t-b} & 0 & -\frac{t-b}{t+b} \cr 0 & 0 & \frac{f+n}{n-f} & \frac{2fn}{n-f} \cr 0 & 0 & -1 & 0 \end{array}\end{pmatrix} $$
视角(Field of View)和长宽比(Aspect Ratio)
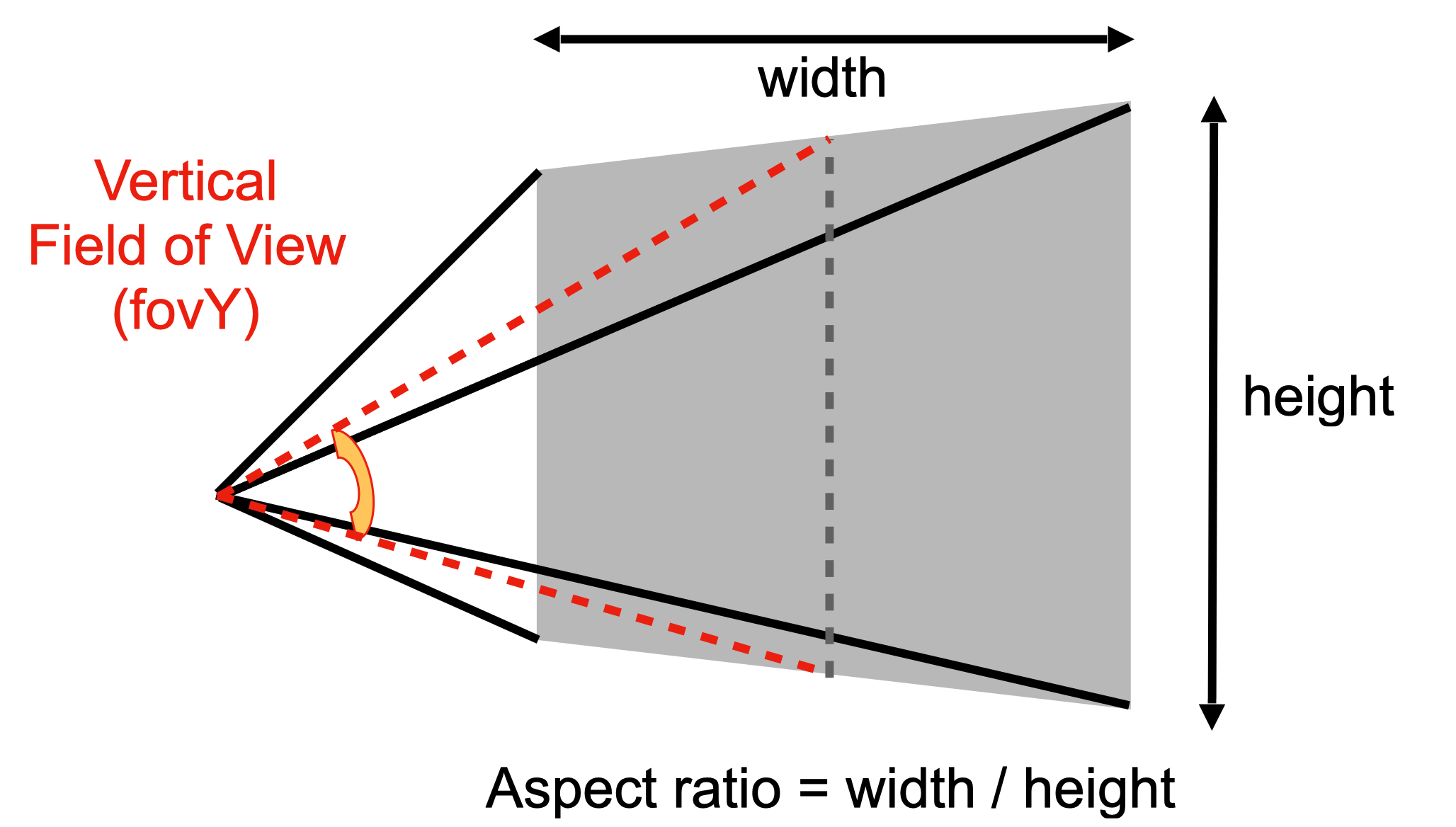
fovY是从摄像机焦点到n平面的t和b线段中点所形成的夹角。长宽比为长/宽。
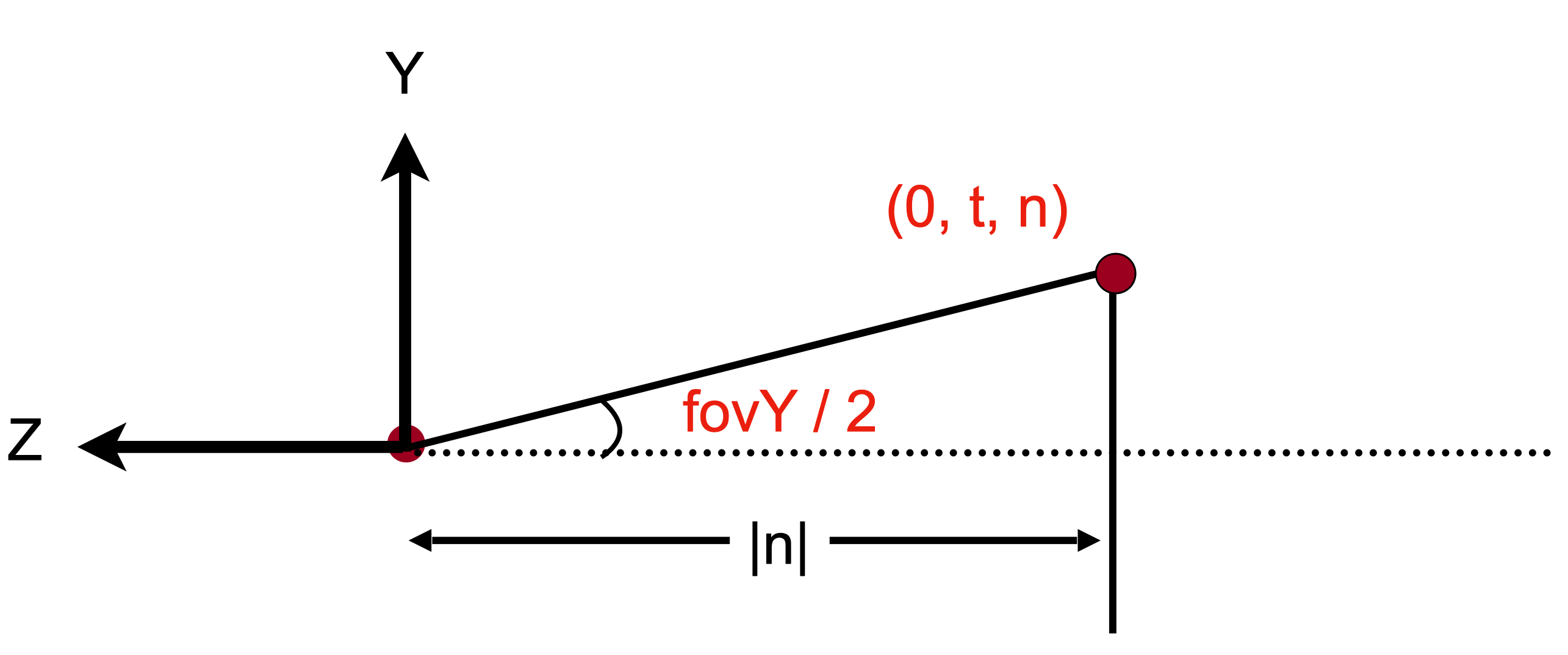
因此我们可以得到
$$ \begin{aligned} \tan \frac{f o v Y}{2} & =\frac{t}{|n|} \cr \text { aspect } & =\frac{r}{t} \end{aligned} $$
光栅化
视口变换
MVP变换的作用是把所有的物体都放在$[-1, 1]^3$的空间中,一旦拥有了这个空间,我们需要进行光栅化以将其显示在屏幕上。
屏幕空间:由像素的二维矩阵组成
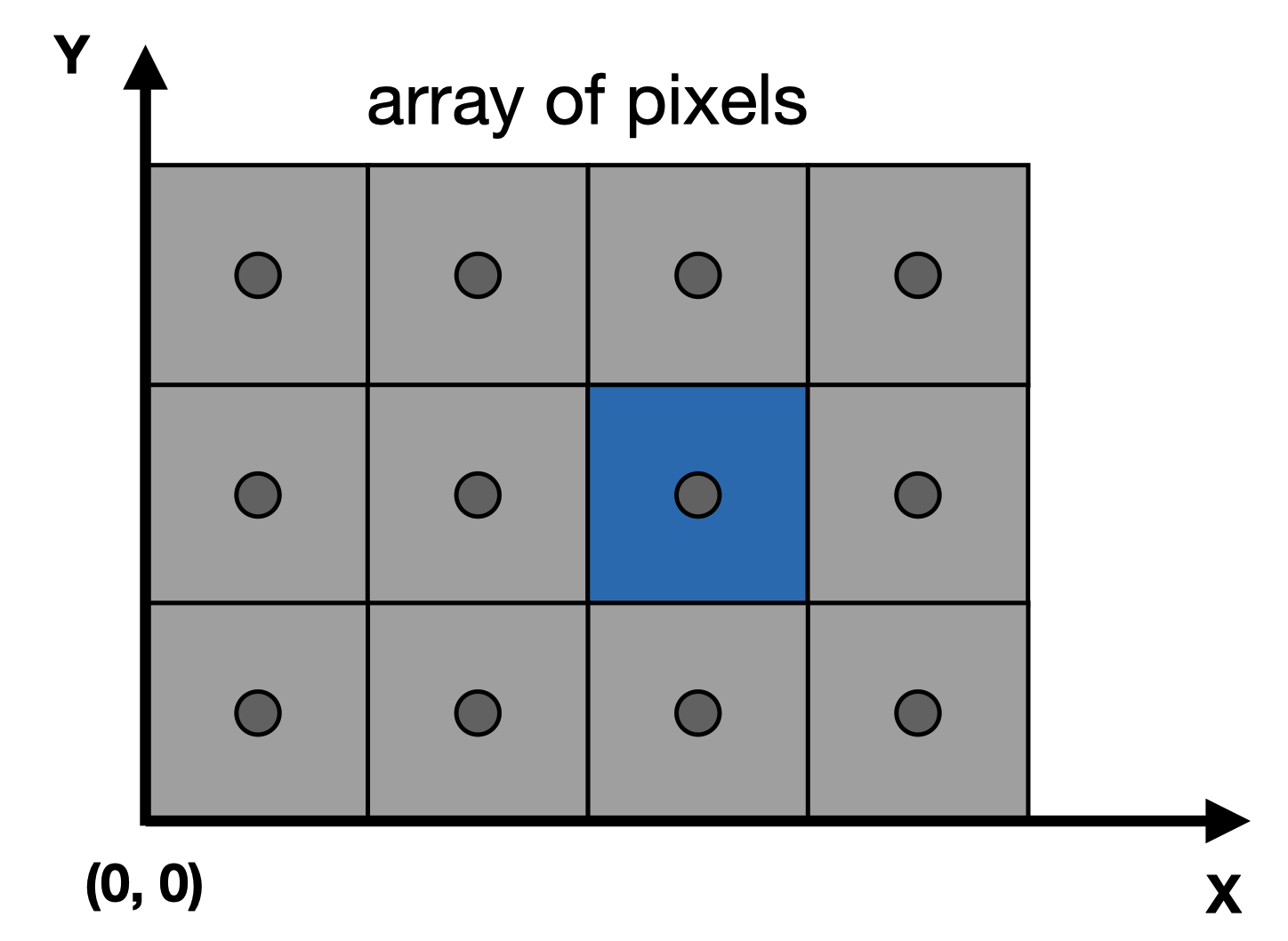
首先不管z,我们先将$[-1,1]^2$变换到$[0, width] \times [0, height]$的二维平面上,这叫做视口变换(viewport transform)
$$ M_{\text {viewport }}=\left(\begin{array}{cccc} \frac{\text { width }}{2} & 0 & 0 & \frac{\text { width }}{2} \cr 0 & \frac{\text { height }}{2} & 0 & \frac{\text { height }}{2} \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \end{array}\right) $$
光栅化2D采样
得到视口变换后,我们需要告诉每个像素点颜色是什么,即将连续的模型变为离散的像素点,这就是光栅化。
当经过MVP变换后拥有三角形的三个顶点坐标后,如何判断每个像素的颜色?
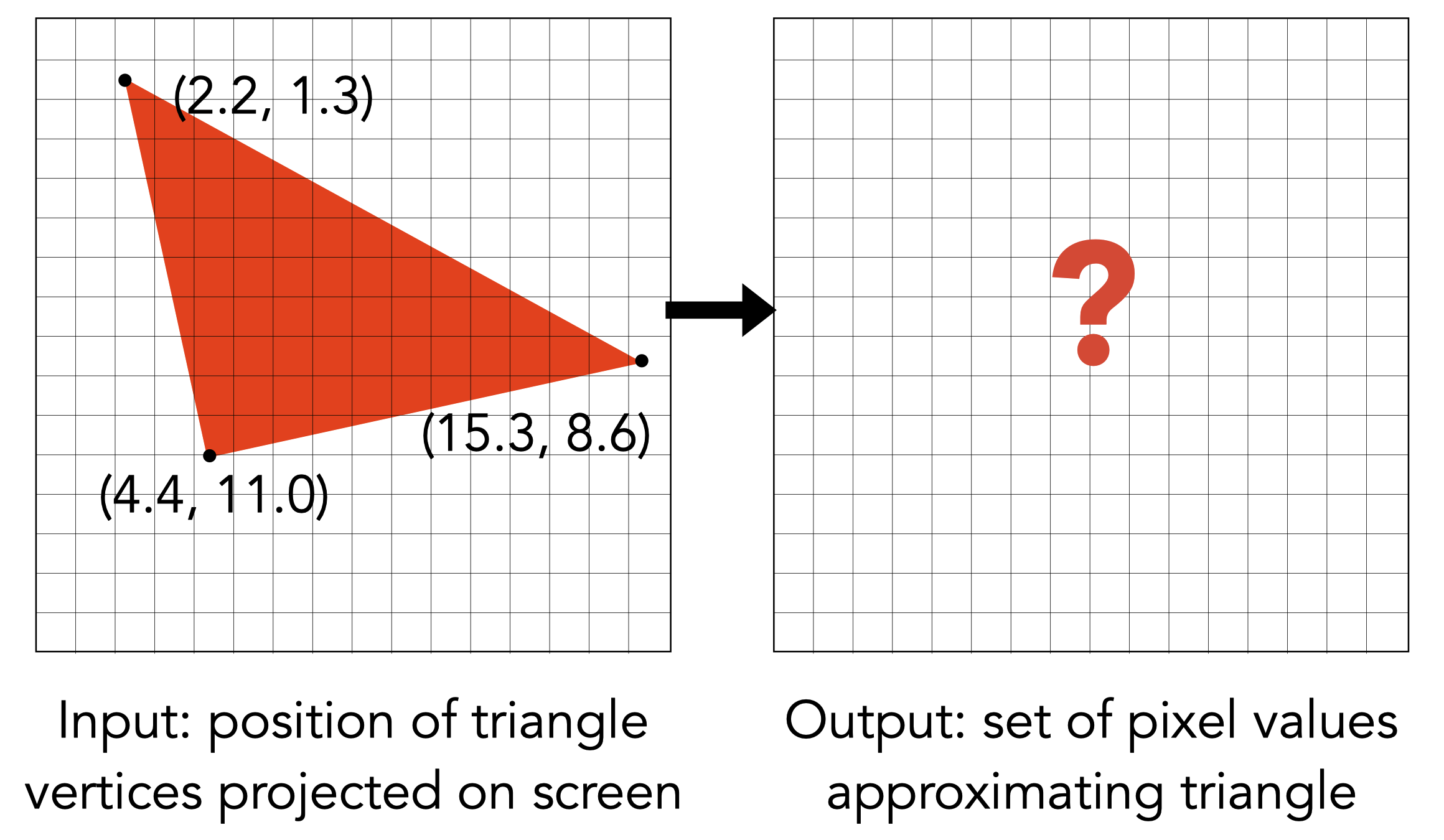
利用像素中心对屏幕空间进行采样,即判断每个像素中心是否在三角形内
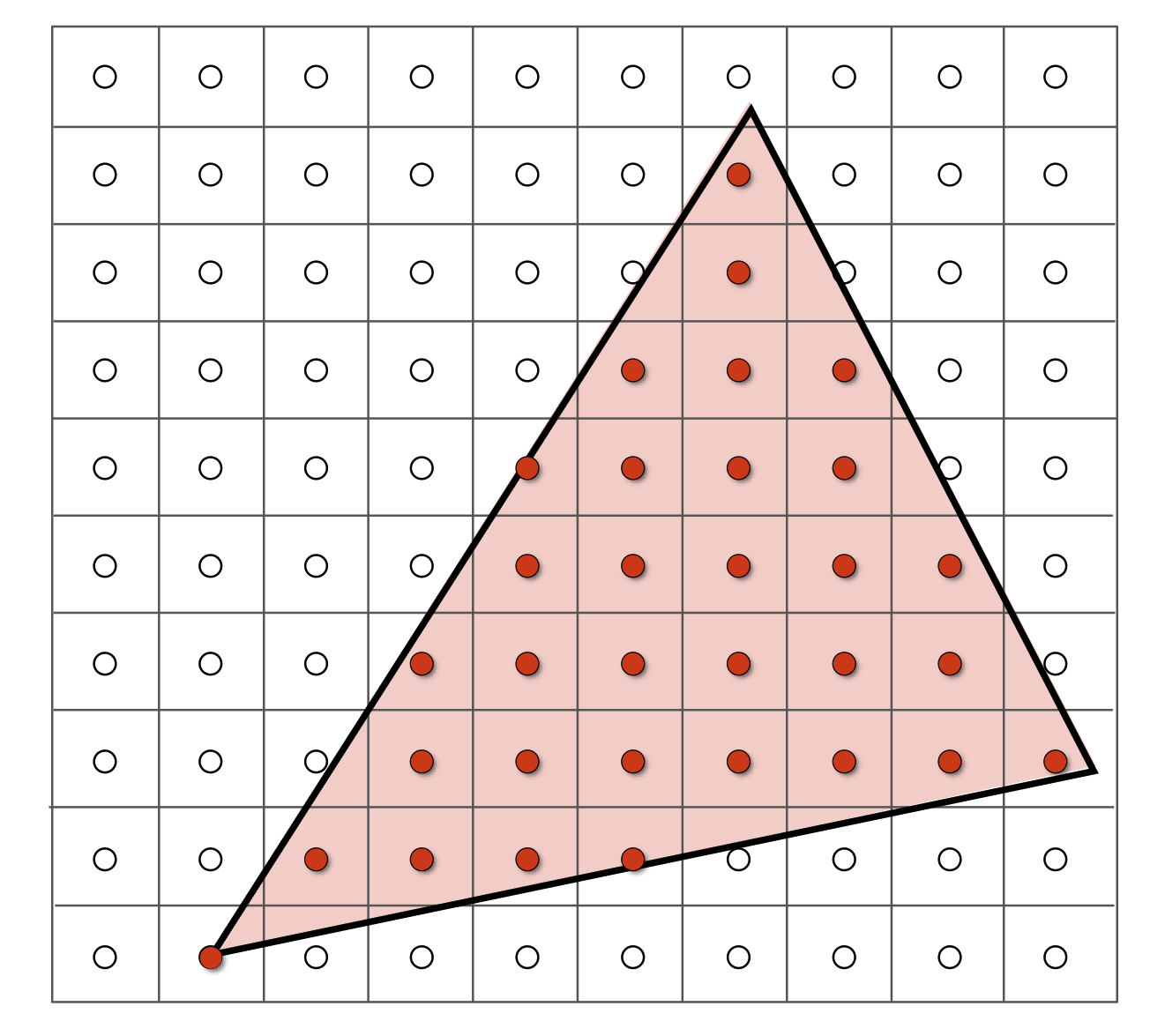
如何判断一个点是否在三角形内?
判断$\overrightarrow{QP_0} \times \overrightarrow{P_0P_1}, \overrightarrow{QP_1} \times \overrightarrow{P_1P_2}, \overrightarrow{QP_2} \times \overrightarrow{P_2P_0}$的符号,如果他们的符号都相同,那么这个点在三角形内,否则这个点在三角形外。
走样(aliasing)

反走样 (Anti-aliasing)
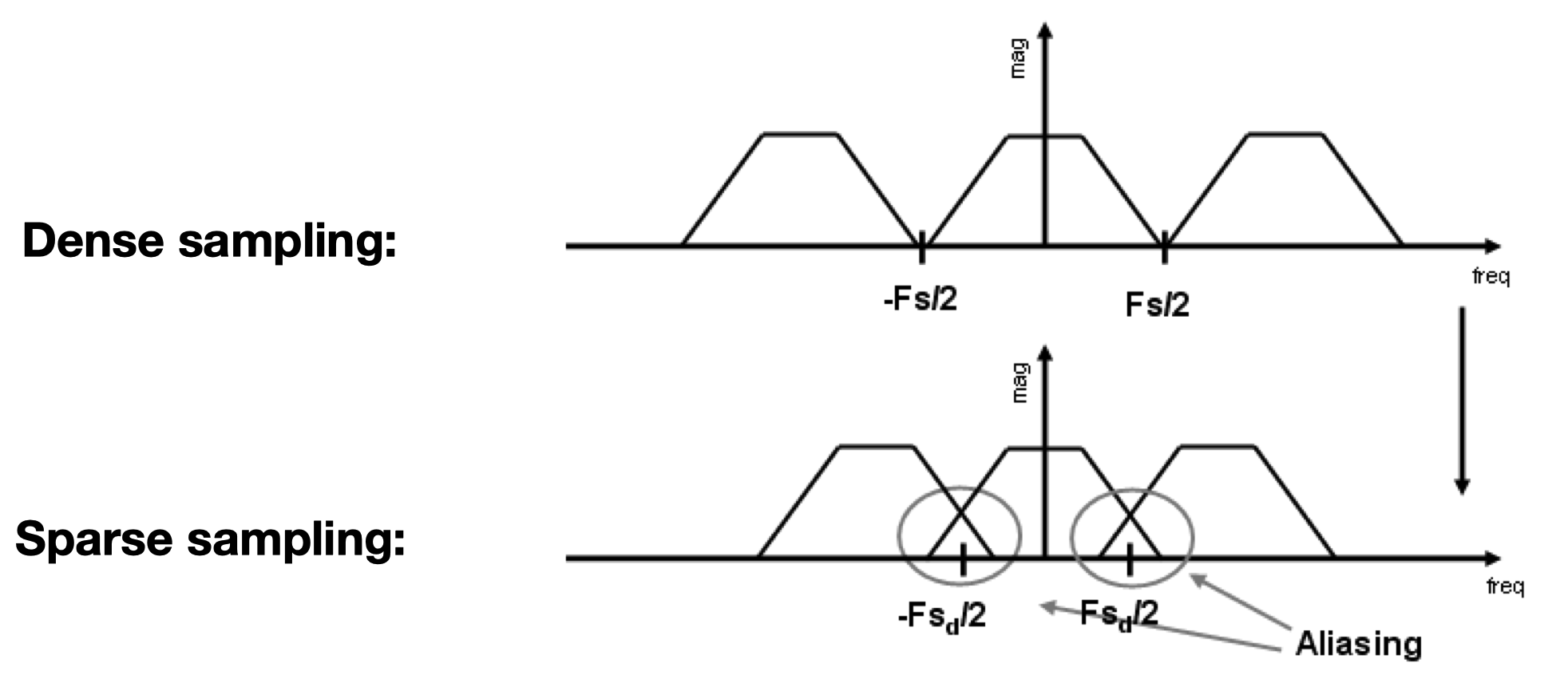
产生走样的原因:信号频率过高(三角形边界的颜色变化太快),采样频率过低,导致高频分量和低频分量的采样结果无法区分(aliasing)
如何进行反走样:在采样前进行模糊/低通滤波(将Nyquist频率以上的信号进行滤波)
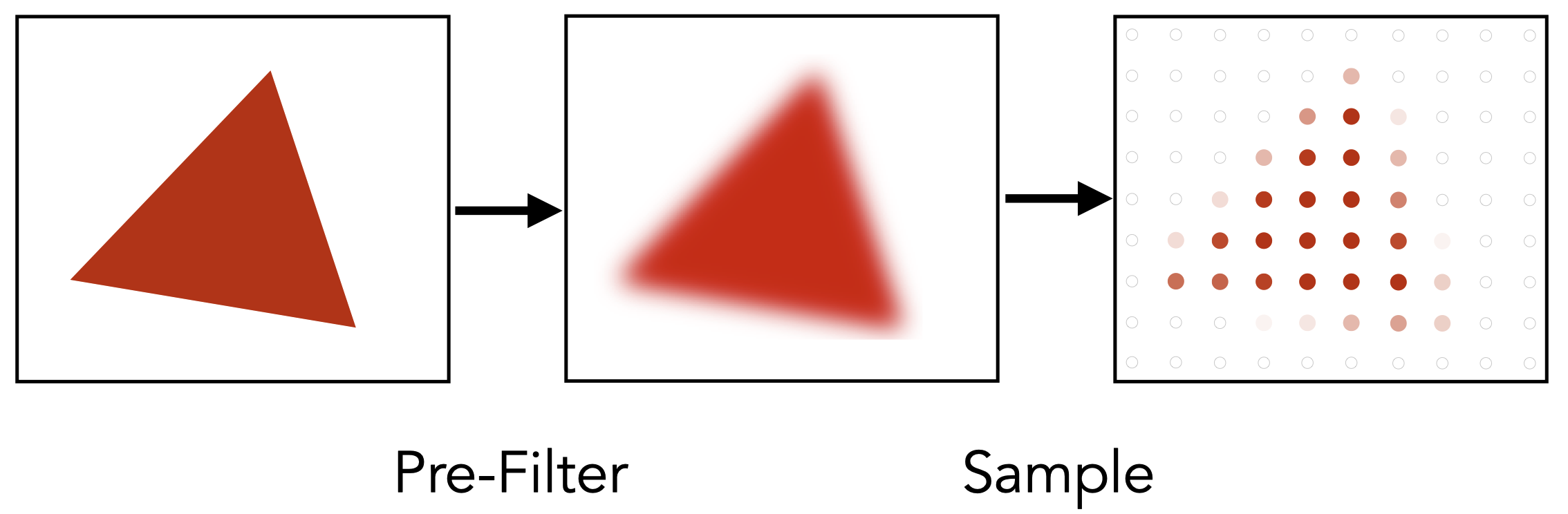
低通滤波的方法:平均/卷积
时域上两个信号的卷积是频域上两个信号的乘积,如下图所示,可以看到只有低频的分量被保留
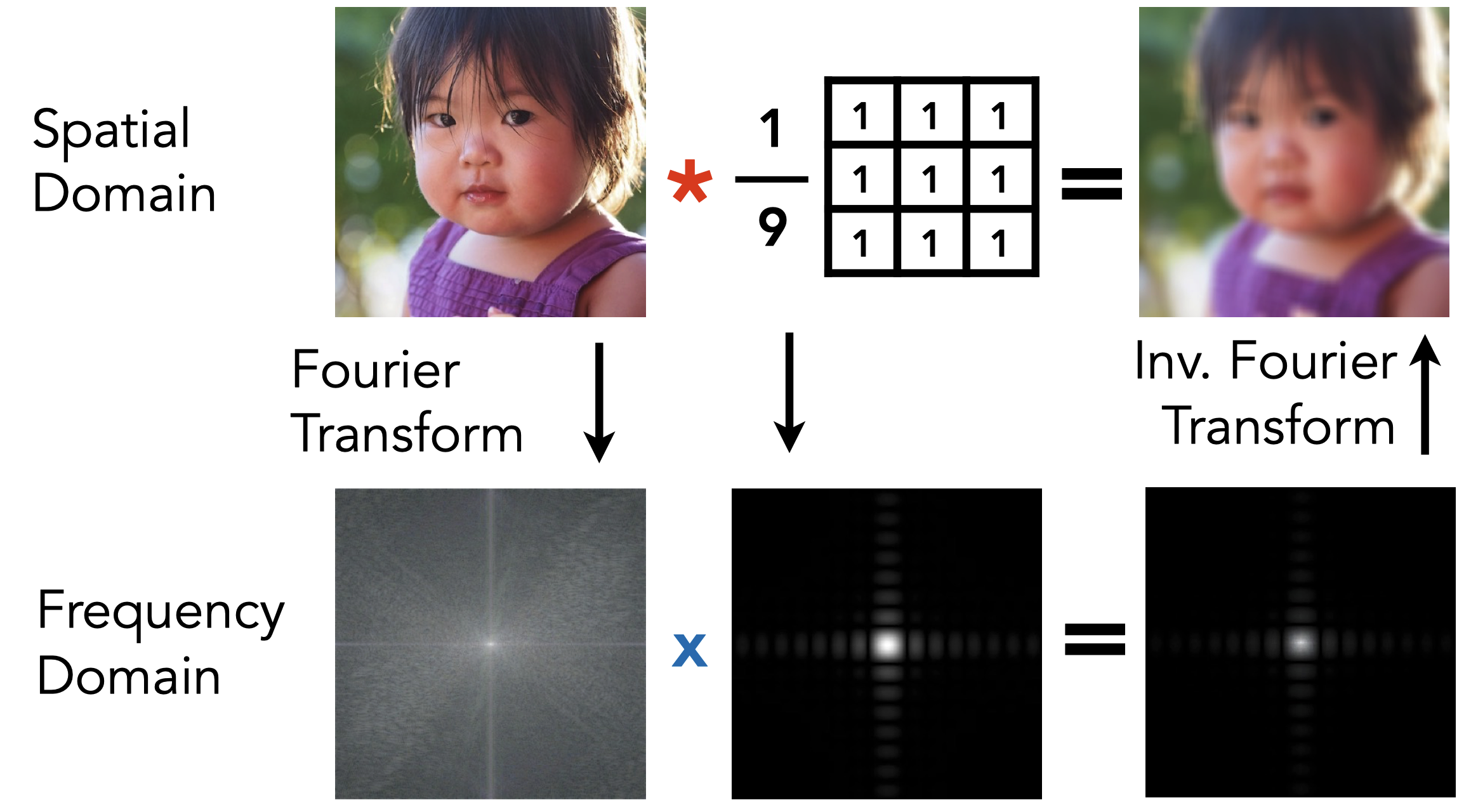
卷积核尺寸越大,保留的频率越低。
采样走样的本质:频谱混叠
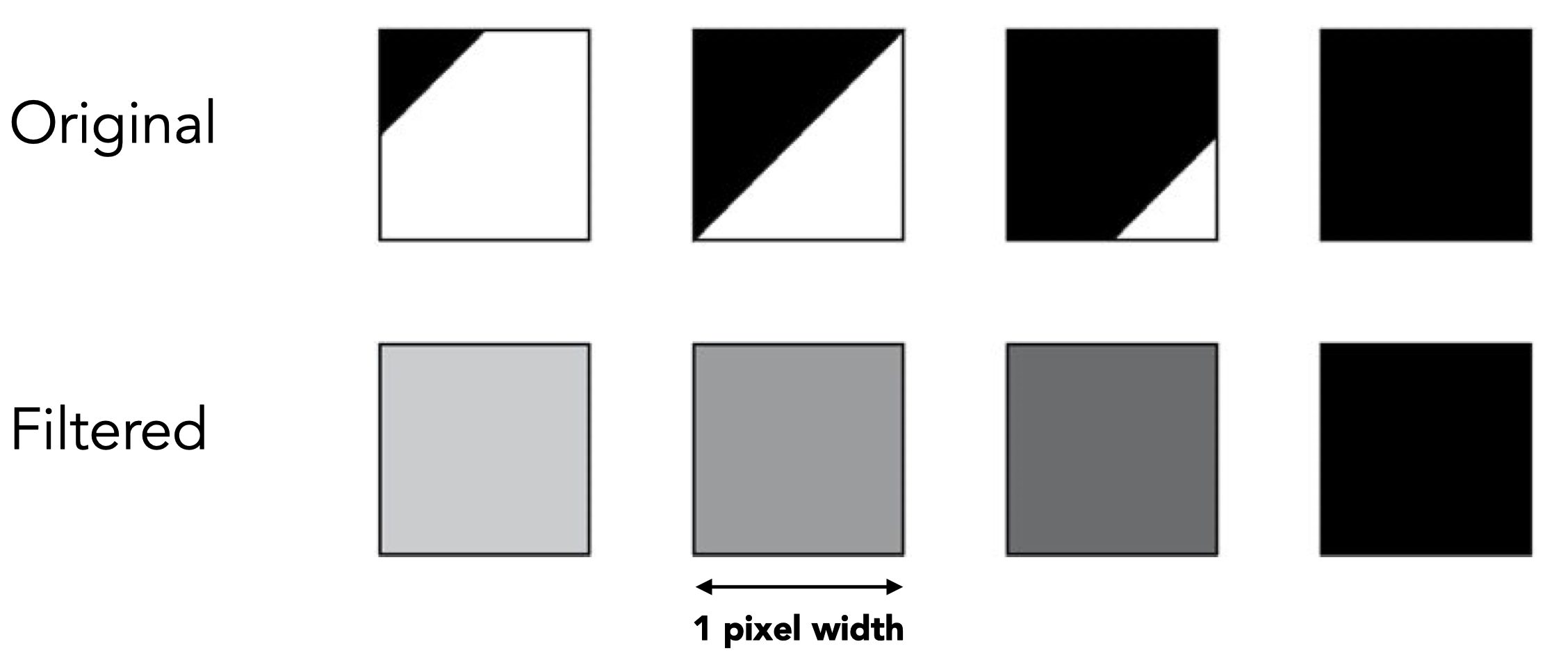
求平均进行反走样的方法:计算每个像素点中在三角形内部的面积,这个面积占总像素的面积比决定了该像素的颜色值
多重采样抗锯齿(Multisample Anti Aliasing, MSAA)
上面的方法其实很难计算,我们需要用近似算法来计算每个像素的覆盖面积比。
MSAA: 将每一个像素点分为多个区域,判断每个小像素点是否在三角形内,从而近似计算像素点在三角形内的平均面积
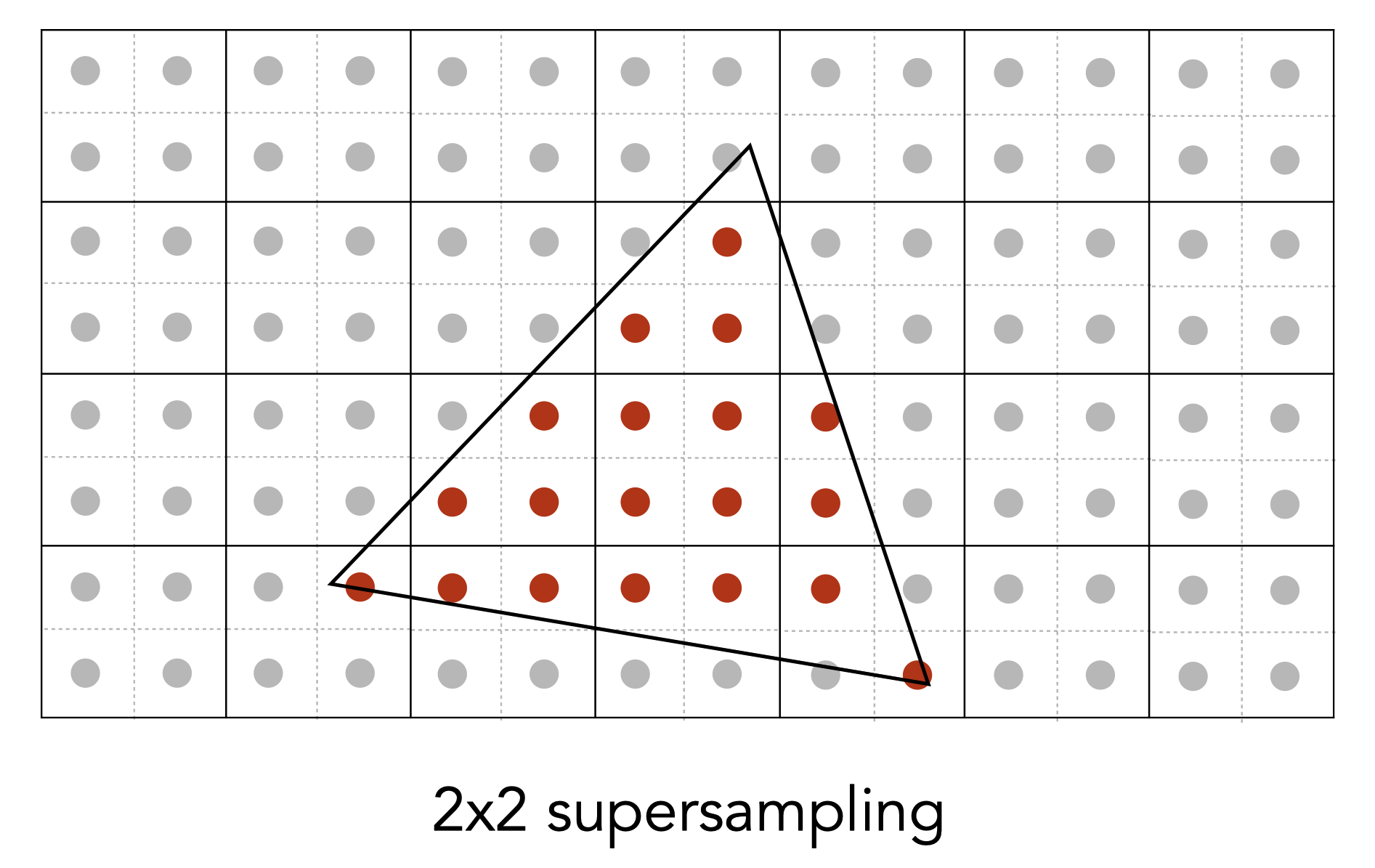
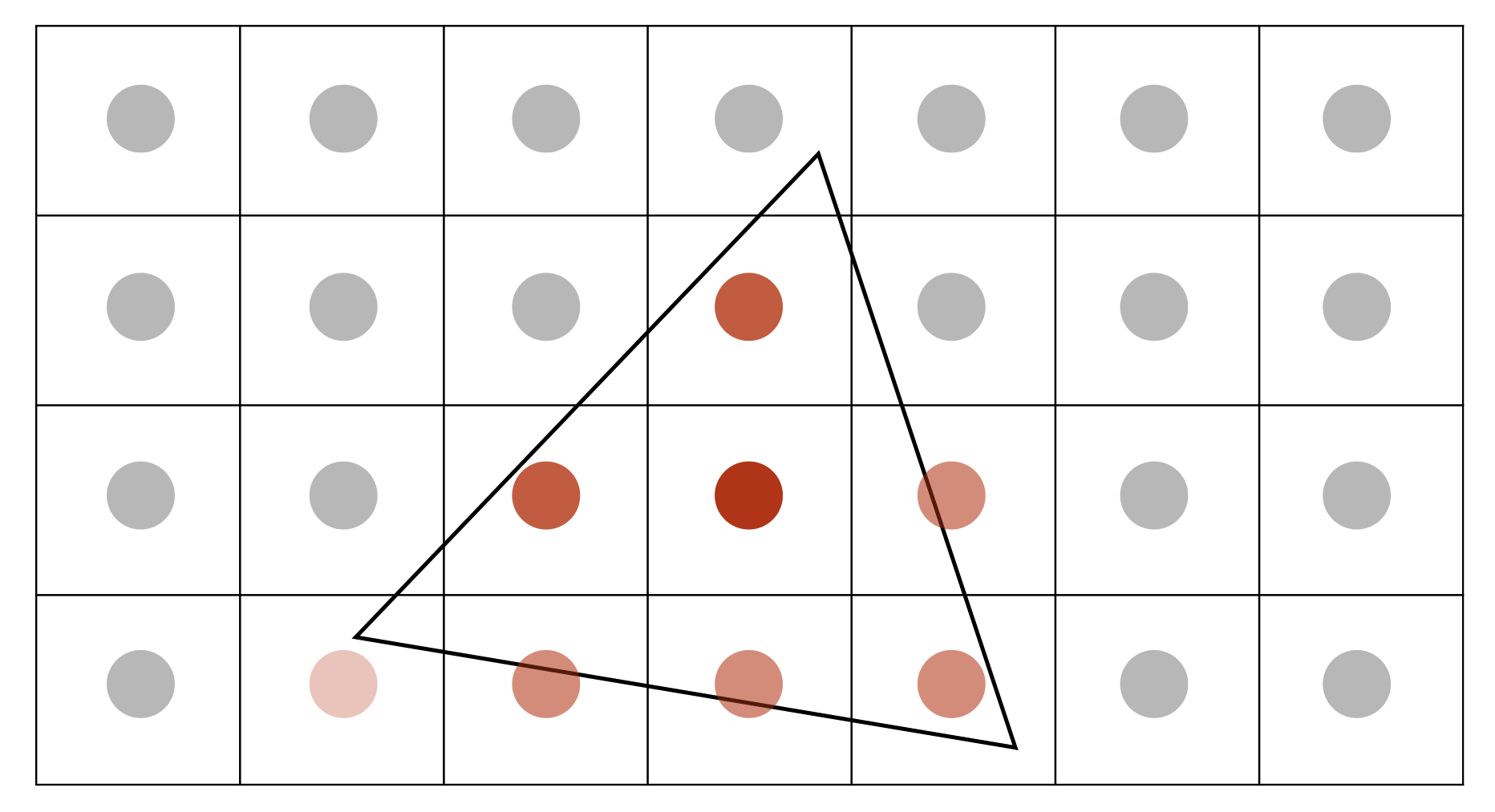
MSAA解决的只是近似计算像素覆盖率问题,而并没有提高采样率。
Z-Buffering
如何处理远近遮挡物体的光栅化?
记录每个像素最小的z值(离相机最近的点)。需要一个深度缓存来记录这个深度值。
为了方便理解,这里定义z都是正值,越小的z表示越近,越大的z表示越远。

着色
着色(Shading):对不同的物体应用不同的材质
为了计算一个shading point的像素颜色,我们需要以下输入:
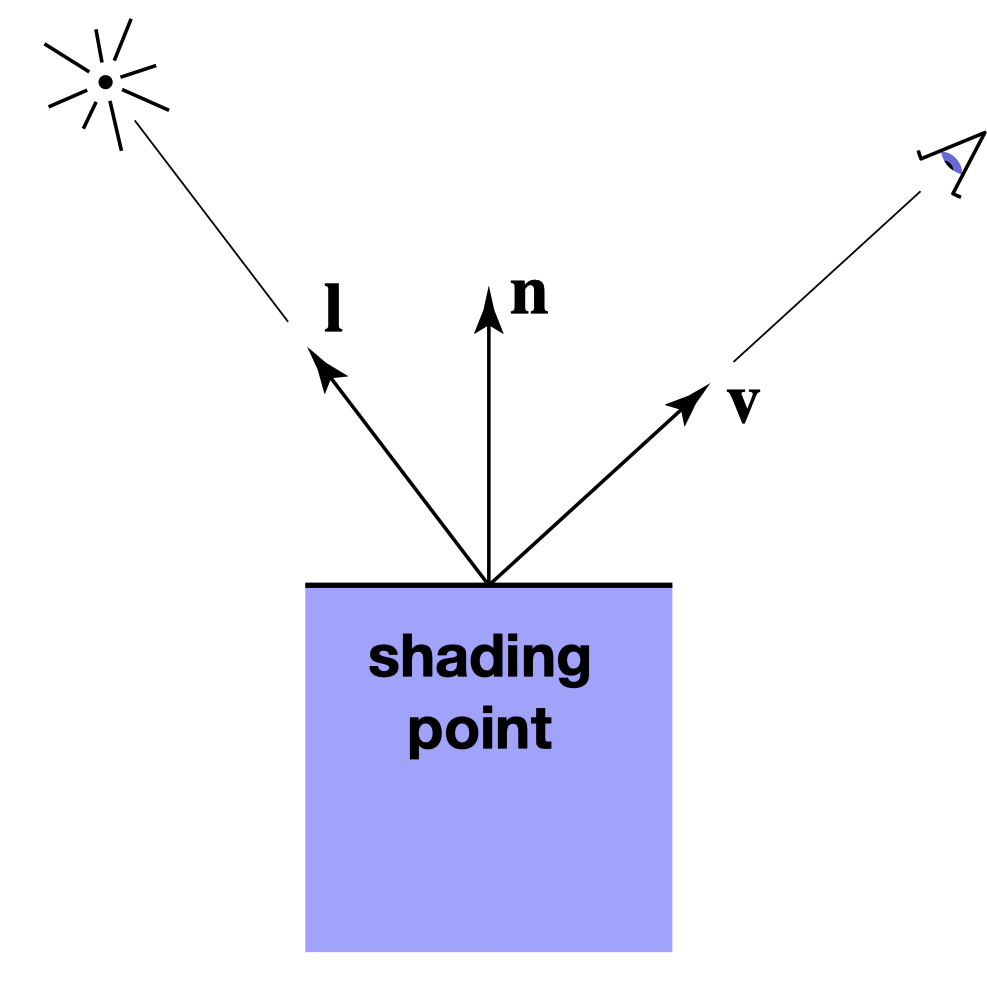
- 观察方向$\vec{v}$
- 表面法线方向$\vec{n}$
- 光源方向$\vec{l}$
- 表面参数,如颜色,粗糙度等
漫反射: 光源向四面八方均匀反射
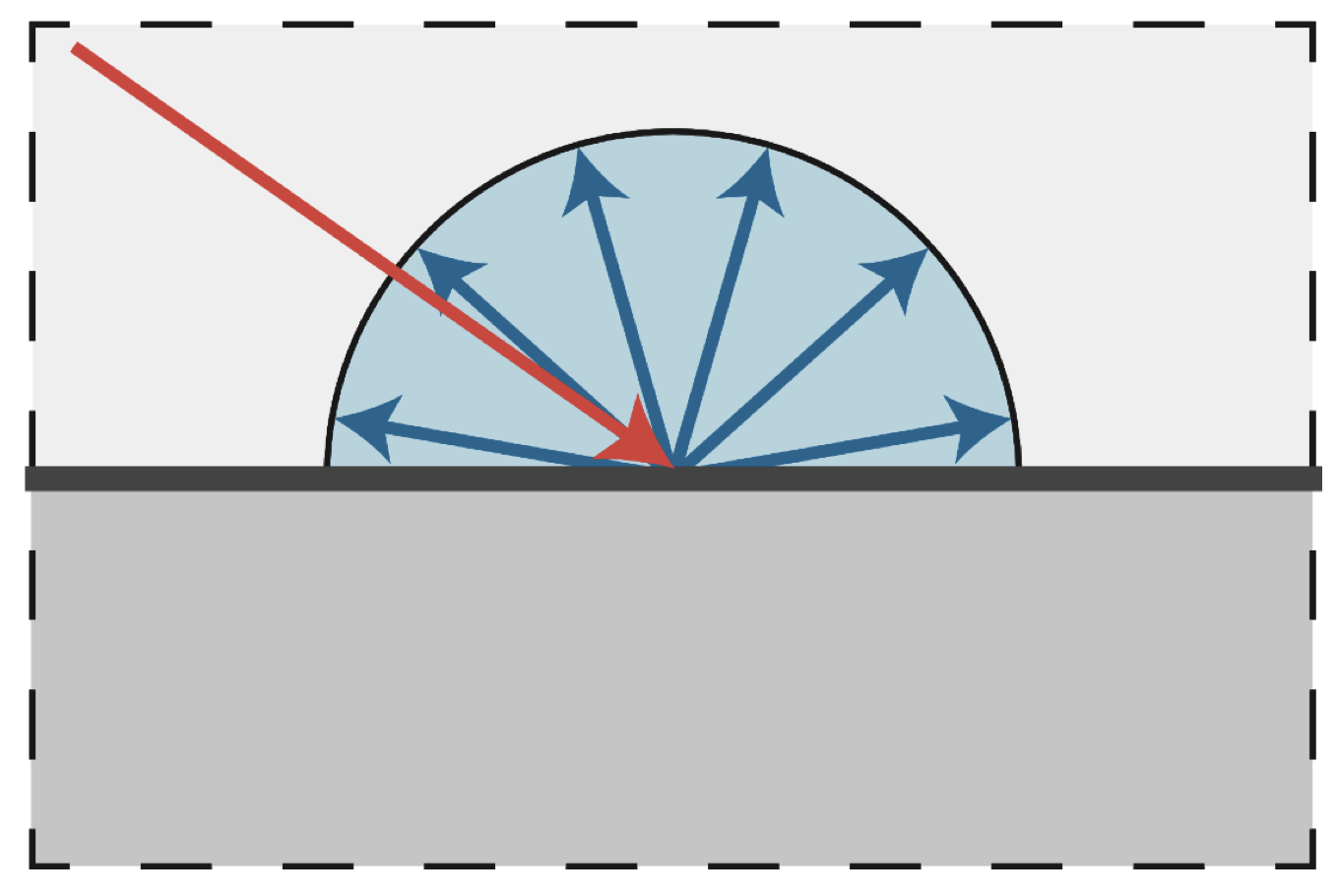
Lambert余弦定理:每单位平面接收到逛的能量和光线与平面法线方向角度的余弦值成正比
同时到达距离光源为$r$的能量和$r^2$成反比,因此我们可以定义漫反射在某一个shading point的能量为 $$ L_d=k_d\left(I / r^2\right) \max (0, \mathbf{n} \cdot \mathbf{l}) $$ 其中$I / r^2$是到达shading point的能量,$\max (0, \mathbf{n} \cdot \mathbf{l})$是被shading point接收的能量,$k_d$是漫反射系数。由于漫反射向四面八方反射完全相同,因此漫反射的能量和观测方向无关。
高光(Specular)
当观察方向和光线的镜面反射方向接近时可以看到高光部分。
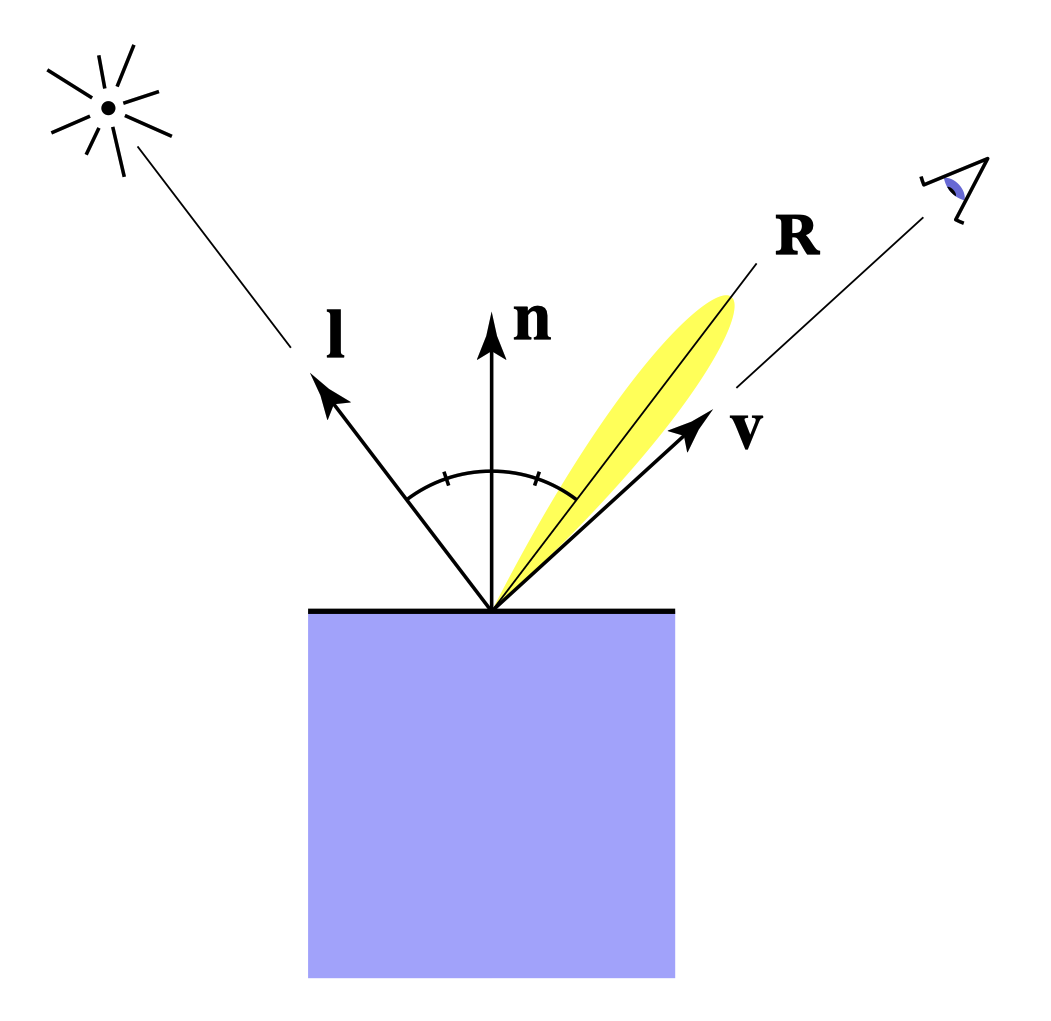
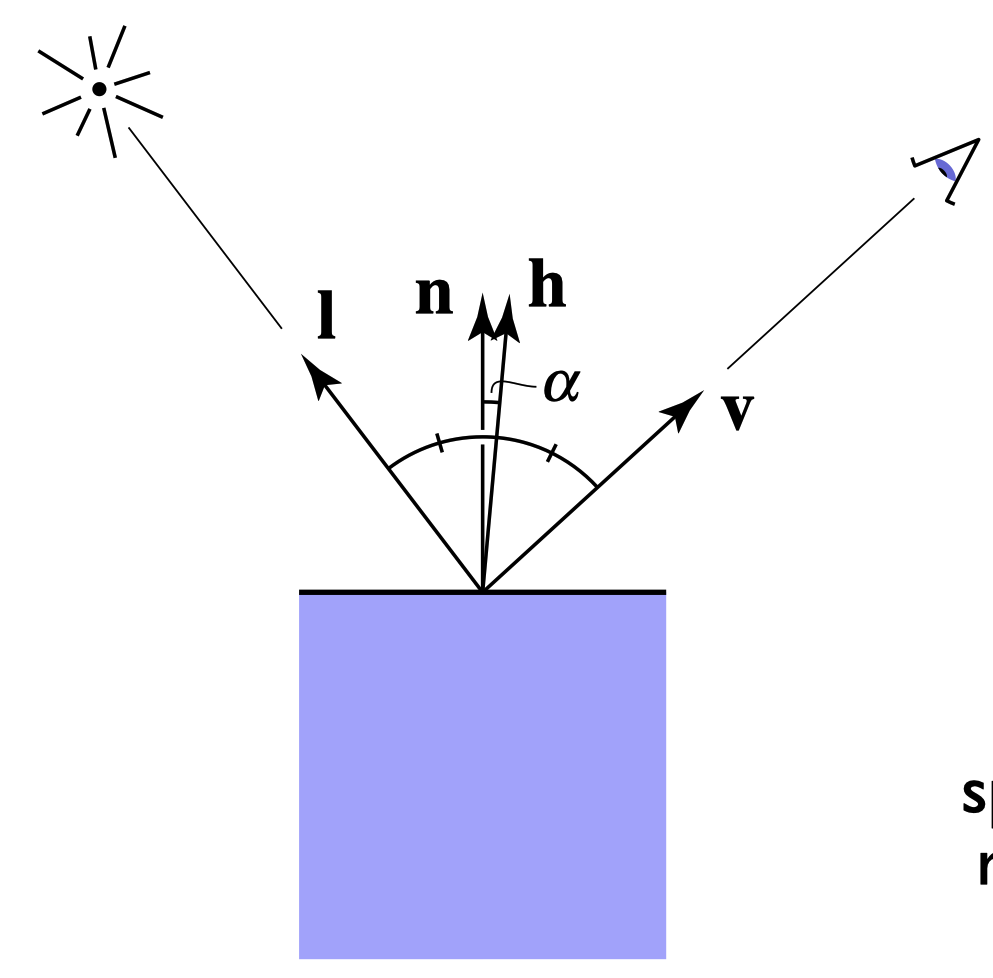
当半程向量$\mathbf{h}$($\mathbf{l}$和$\mathbf{v}$的平分向量)和法线$\mathbf{n}$接近时可以看到高光。 $$ \begin{aligned} & \underset{(\text { 半程向量) }}{\mathbf{h}} = \operatorname{bisector}(\mathbf{v}, \mathbf{l}) \cr & \quad=\frac{\mathbf{v}+\mathbf{l}}{|\mathbf{v}+\mathbf{l}|} \end{aligned} $$
Blinn-Phong模型中高光项的公式: $$ \begin{aligned} & L_s=k_s\left(I / r^2\right) \max (0, \cos \alpha)^p \cr & =k_s\left(I / r^2\right) \max (0, \mathbf{n} \cdot \mathbf{h})^p \cr \end{aligned} $$ 其中$L_s$表示高光项,$k_s$表示高光系数,$p$指数项是为了让当$\mathbf{h}$和$\mathbf{n}$较远时高光项迅速减少,这个数一般是100-200。
环境光(Ambient Term)
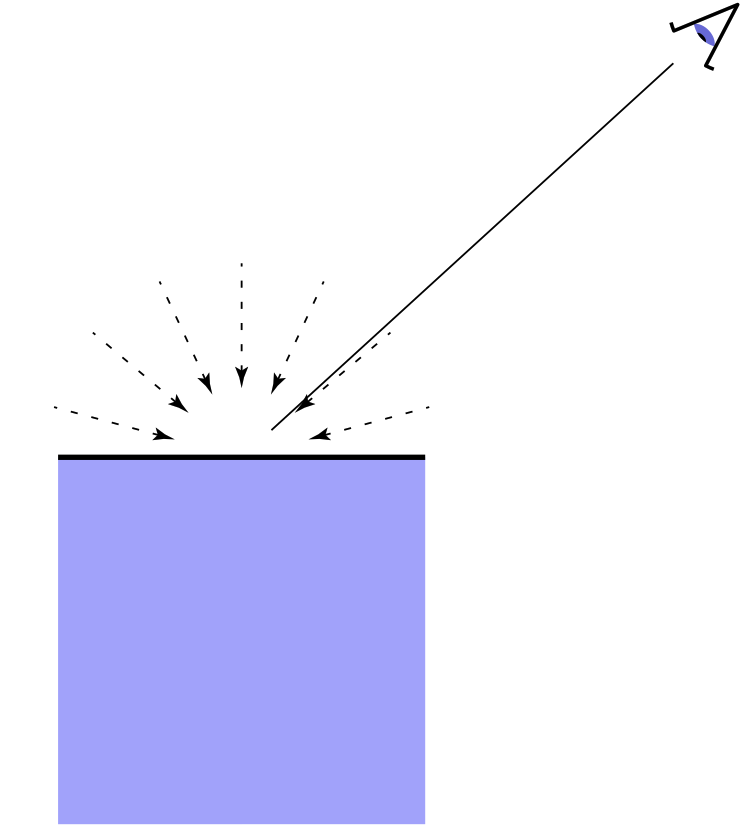
简化情况下,环境光基本可以被认为是一个常数。 $$ L_a=k_a I_a $$
Blinn-Phong反射模型
Blinn-Phong反射=环境光+漫反射+高光 $$ \begin{aligned} L & =L_a+L_d+L_s \ & =k_a I_a+k_d\left(I / r^2\right) \max (0, \mathbf{n} \cdot \mathbf{l})+k_s\left(I / r^2\right) \max (0, \mathbf{n} \cdot \mathbf{h})^p \end{aligned} $$
着色频率

着色频率表示计算着色点的频率。第一个小球是对每一个面进行着色(flat shading),第二个小球是对每一个顶点计算法线然后着色(Gouraud shading),最后一个小球是对每一个像素点进行着色(Phong shading)。
如何计算逐顶点的法线向量
计算这个顶点周围的三角形的法线平均
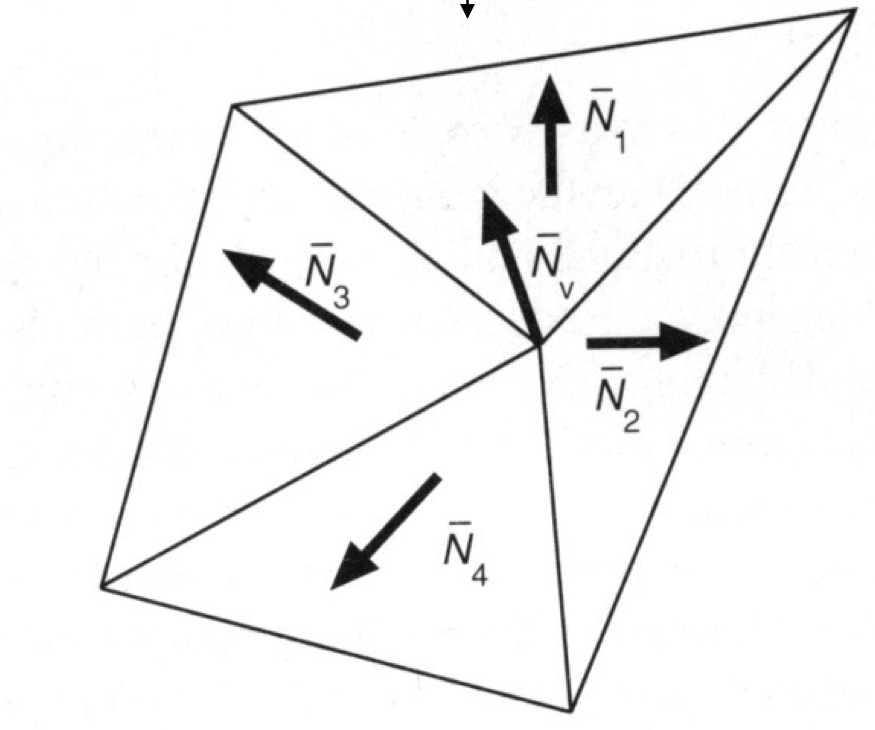 $$
N_v=\frac{\sum_i N_i}{\left|\sum_i N_i\right|}
$$
为了实现更好的效果,可以根据相邻三角形的面积大小求加权平均。
$$
N_v=\frac{\sum_i N_i}{\left|\sum_i N_i\right|}
$$
为了实现更好的效果,可以根据相邻三角形的面积大小求加权平均。
如何计算逐顶点的法线向量
Barycentric插值,后面会提到。
实时渲染管线
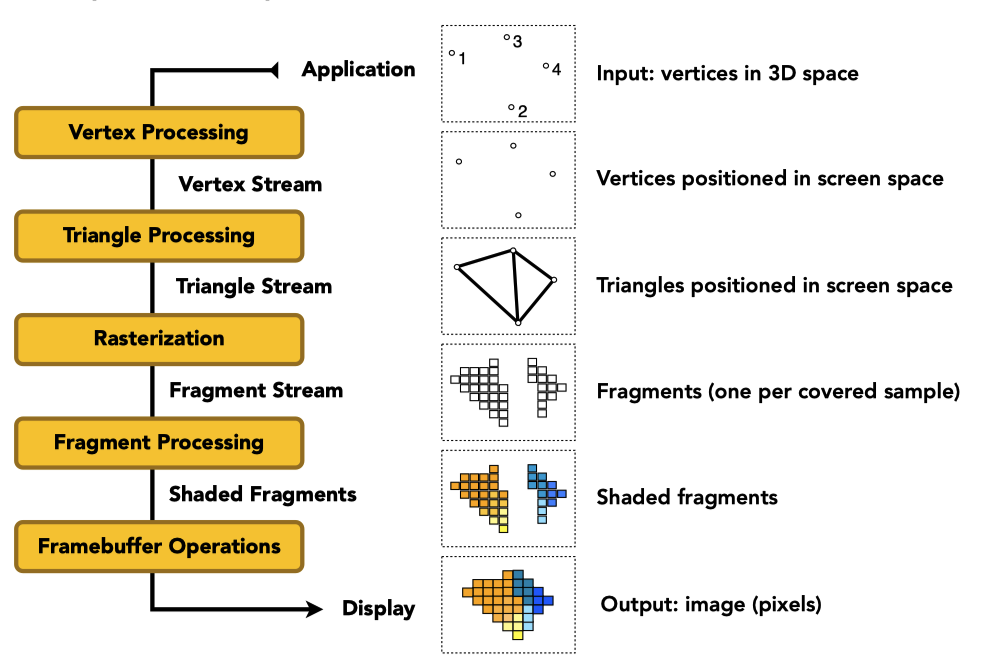
Shader: 自定义顶点或像素着色效果的代码块,描述了一个顶点或像素的操作(不需要写for循环)。描述顶点着色的叫顶点着色器(vertex shader),描述像素的叫像素/片段着色器(fragment shader)
一个GLSL片段着色器计算Phong模型简化版漫反射的示例:
uniform sampler2D myTexture;
uniform vec3 lightDir;
varying vec2 uv;
varying vec3 norm;
void diffuseShader() {
vec3 kd;
kd = texture2d(myTexture, uv);
kd *= clamp(dot(–lightDir, norm), 0.0, 1.0);
gl_FragColor = vec4(kd, 1.0);
}
纹理映射(Texture Mapping)
定义物体不同位置上的属性(漫反射系数、高光系数等),将物体表面上任何一个点和一张图的像素一一映射。
每个三角形的顶点都要被赋予一个纹理上的坐标系(u, v), 这叫做uv map,u和v一般都在(0, 1)范围内
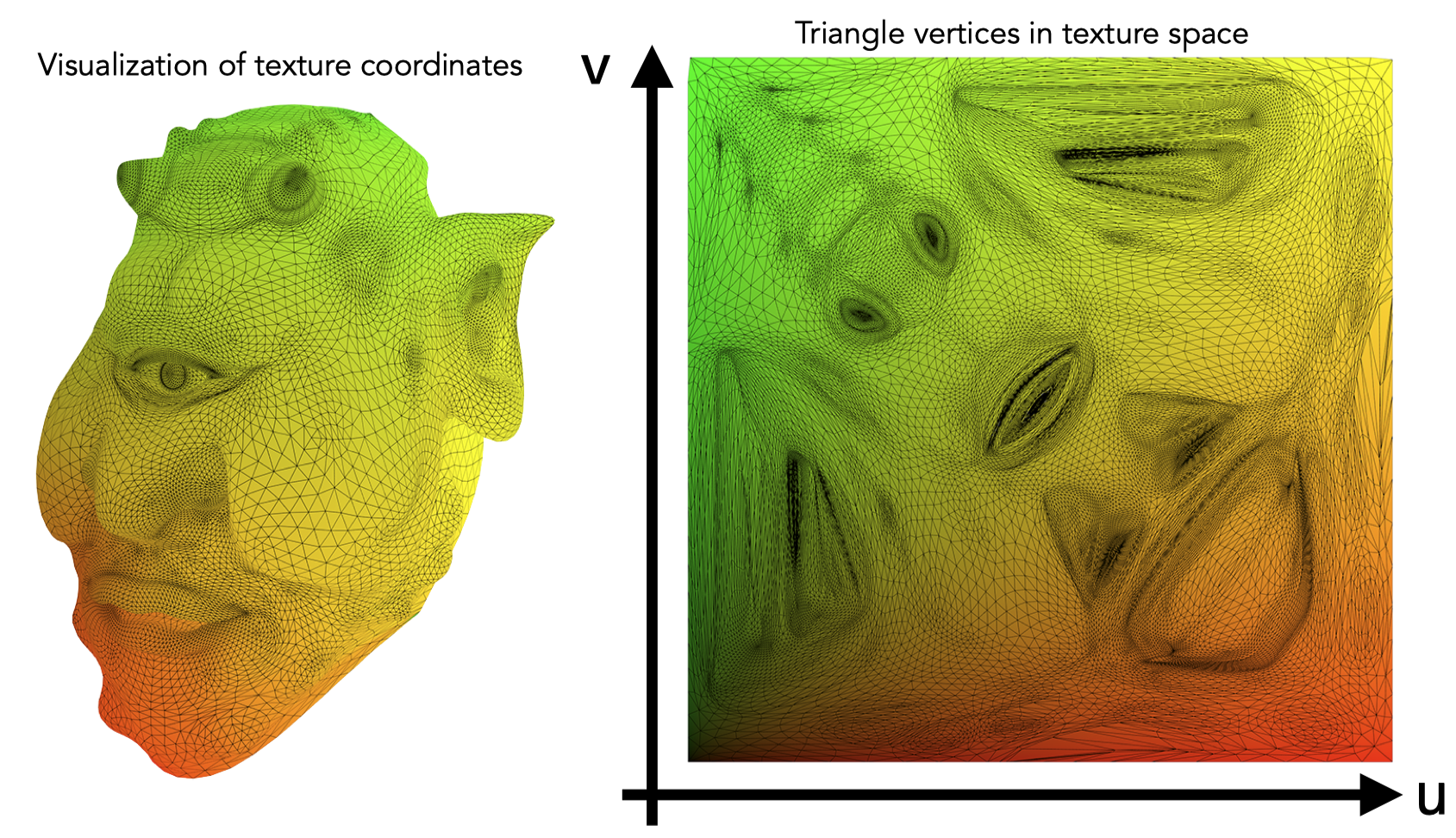
Tilable texture: 四方连续的纹理,当纹理拼接起来的时候是连续的。
重心坐标(Baycentric coordinates)
重心坐标用于计算三角形内的插值以获得三角形内的平滑变化的数据,因为很多时候我们只有三角形顶点上的数据
可以进行插值的属性包括纹理坐标、颜色、法线向量等。
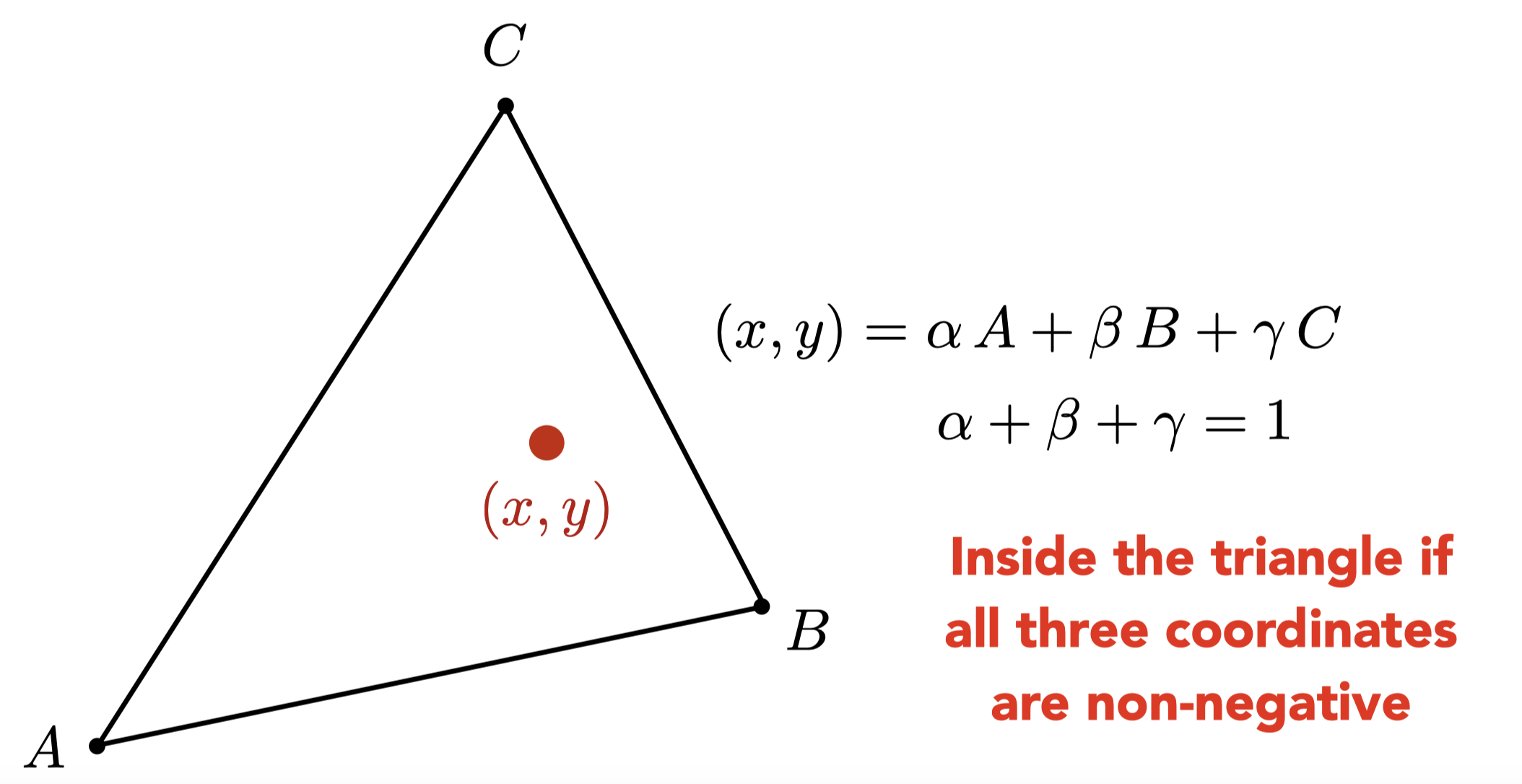
三角形内的任何一个点都可以用$\alpha, \beta, \gamma$的线性组合进行表示,当这三个值都大于等于0时这个点在三角形内部。
计算$\alpha, \beta, \gamma$的方法:通过三角形内部小三角形的面积进行计算:
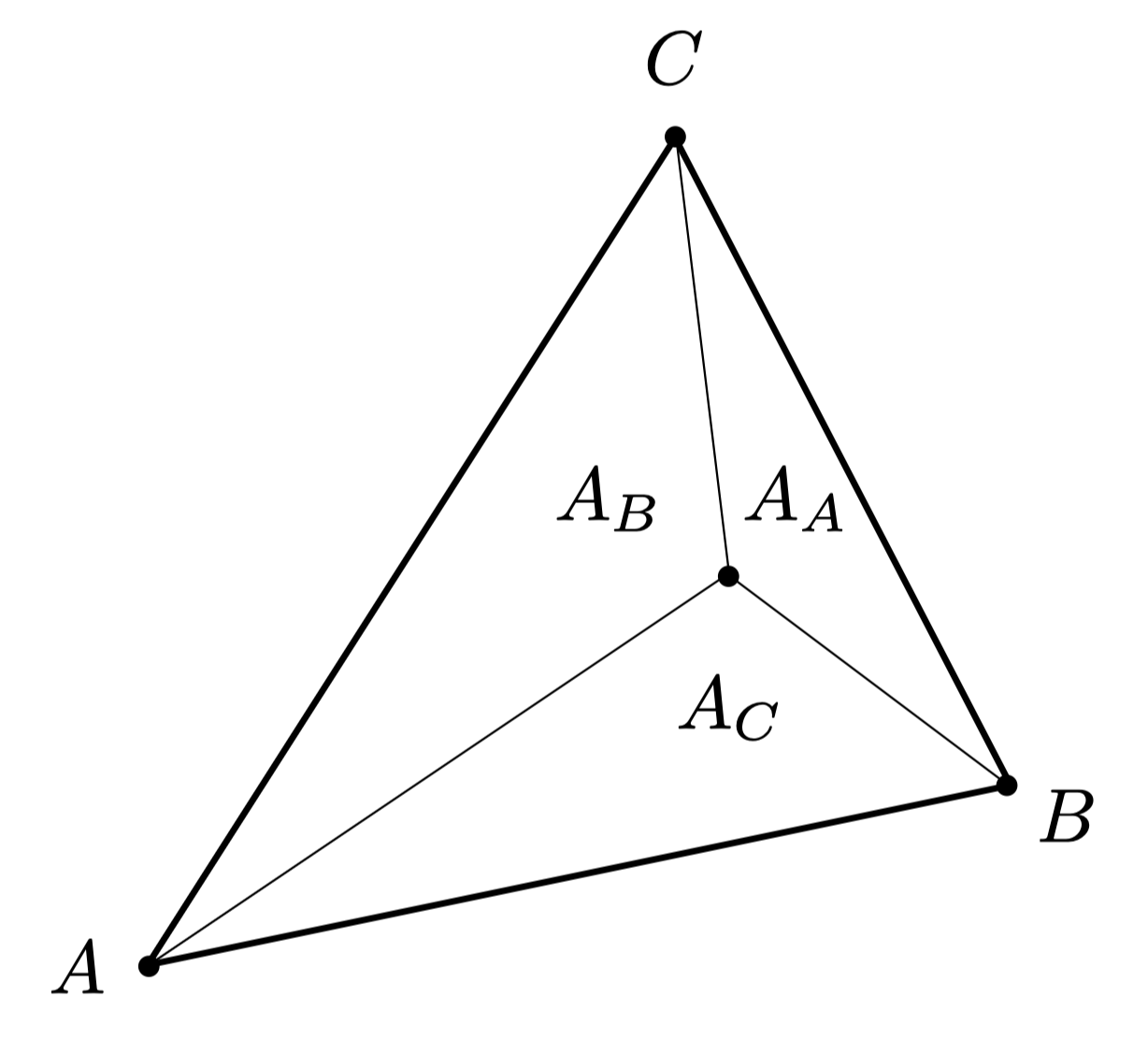 $$
\begin{aligned}
\alpha & =\frac{A_A}{A_A+A_B+A_C} \cr
\beta & =\frac{A_B}{A_A+A_B+A_C} \cr
\gamma & =\frac{A_C}{A_A+A_B+A_C}
\end{aligned}
$$
三角形的重心就是$\alpha=\beta=\gamma = \frac{1}{3}$的情况。
$$
\begin{aligned}
\alpha & =\frac{A_A}{A_A+A_B+A_C} \cr
\beta & =\frac{A_B}{A_A+A_B+A_C} \cr
\gamma & =\frac{A_C}{A_A+A_B+A_C}
\end{aligned}
$$
三角形的重心就是$\alpha=\beta=\gamma = \frac{1}{3}$的情况。
如果知道A, B, C的x,y坐标,那么我们可以用下面的公式计算$\alpha, \beta, \gamma$ $$ \begin{aligned} \alpha & =\frac{-\left(x-x_B\right)\left(y_C-y_B\right)+\left(y-y_B\right)\left(x_C-x_B\right)}{-\left(x_A-x_B\right)\left(y_C-y_B\right)+\left(y_A-y_B\right)\left(x_C-x_B\right)} \cr \beta & =\frac{-\left(x-x_C\right)\left(y_A-y_C\right)+\left(y-y_C\right)\left(x_A-x_C\right)}{-\left(x_B-x_C\right)\left(y_A-y_C\right)+\left(y_B-y_C\right)\left(x_A-x_C\right)} \cr \gamma & =1-\alpha-\beta \end{aligned} $$ 但是要注意,在投影之后重心坐标会发生改变,因此我们必须要在三维空间内的重心坐标计算插值而不能在经过MVP和viewport变换之后再计算重心坐标。我们这里需要用到透视校正插值,得到某个$(\alpha, \beta, \gamma)$重心坐标下正确的深度值为 $$ \frac{1}{z_0} = \alpha\frac{1}{z_1} + \beta\frac{1}{z_2} + \gamma\frac{1}{z_3} $$ 其中$z_0$为透视校正插值后正确的深度值。
顶点属性的正确插值计算方法为 $$ \frac{b_0}{z_0} = \alpha\frac{b_1}{z_1} + \beta\frac{b_2}{z_2} + \gamma\frac{b_3}{z_3} $$ 其中$b_0$为透视校正插值后的正确顶点属性。
纹理放大
如果纹理的分辨率太小可能造成多个pixel对应一个texel(纹理元素、纹素),因而最终会出现模糊的效果。我们可以用双线性插值、双立方插值等方法解决这个问题。
双线性插值
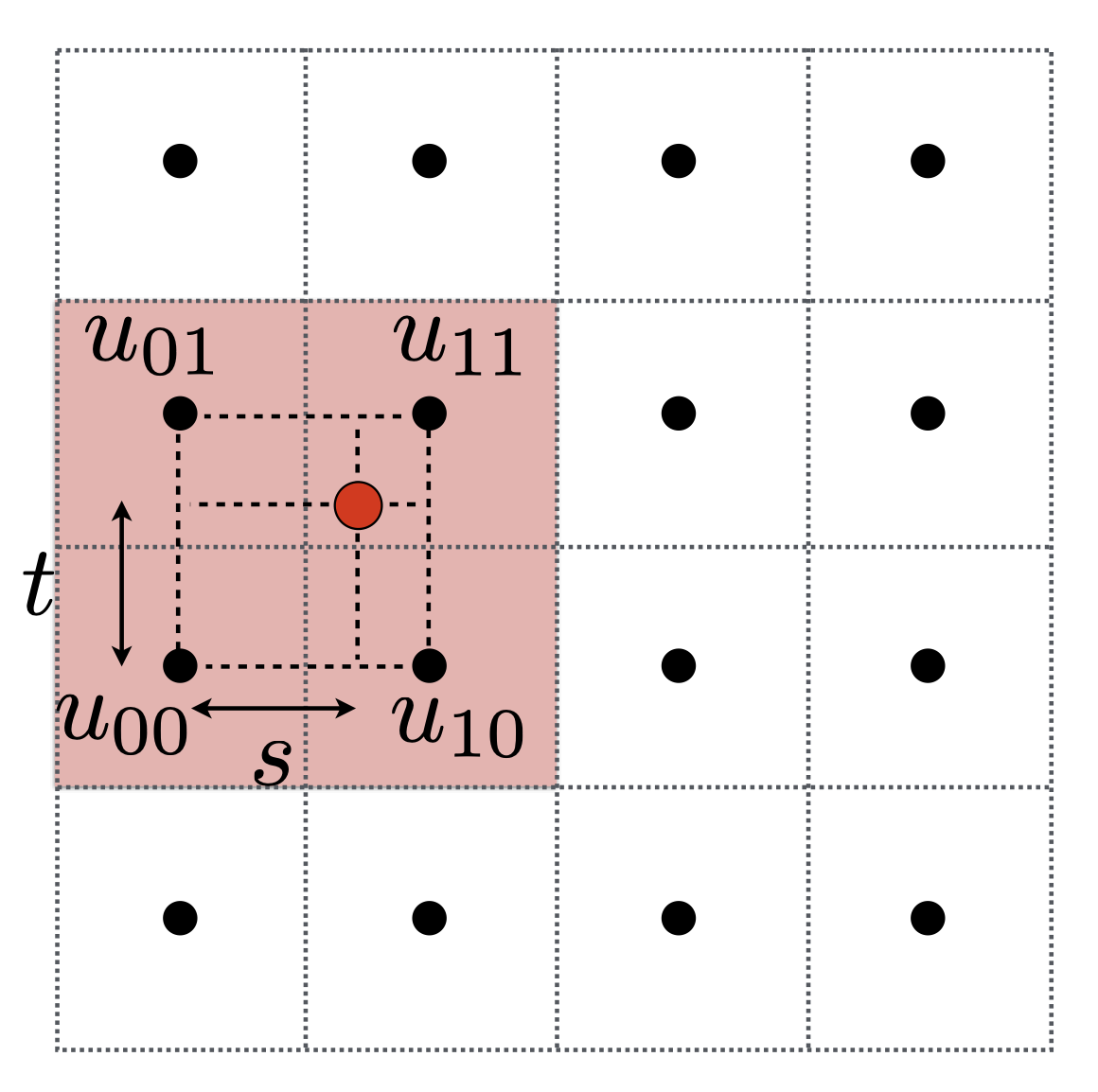
找到pixel对应的uv坐标上周围的四个体素重心,
先用s插值左右两边,得到$u_0$和$u_1$
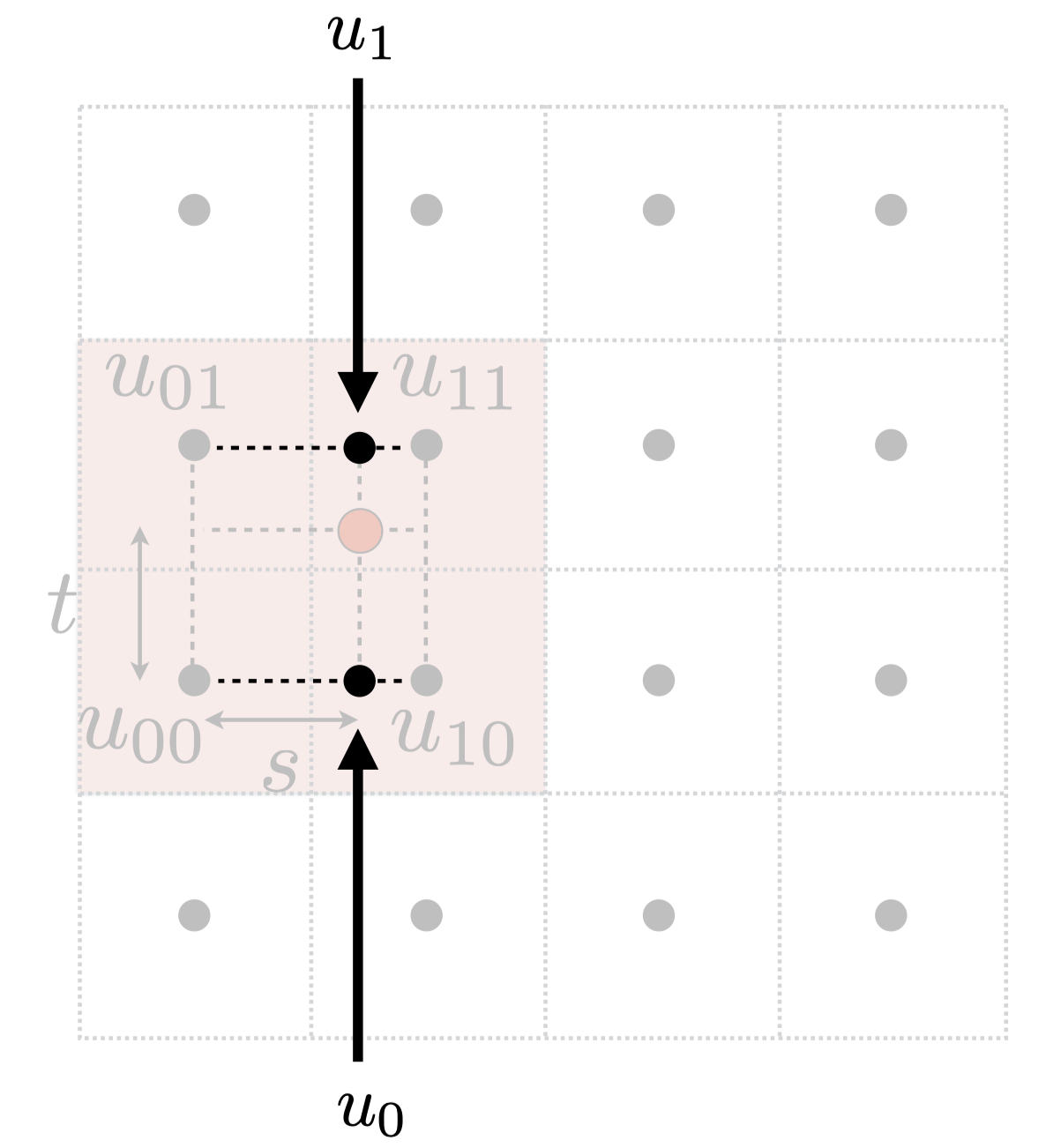 $$
\begin{aligned}
& u_0=\operatorname{lerp}\left(s, u_{00}, u_{10}\right) \cr
& u_1=\operatorname{lerp}\left(s, u_{01}, u_{11}\right)
\end{aligned}
$$
再用t插值上下两边,得到最终的结果
$$
\begin{aligned}
& u_0=\operatorname{lerp}\left(s, u_{00}, u_{10}\right) \cr
& u_1=\operatorname{lerp}\left(s, u_{01}, u_{11}\right)
\end{aligned}
$$
再用t插值上下两边,得到最终的结果
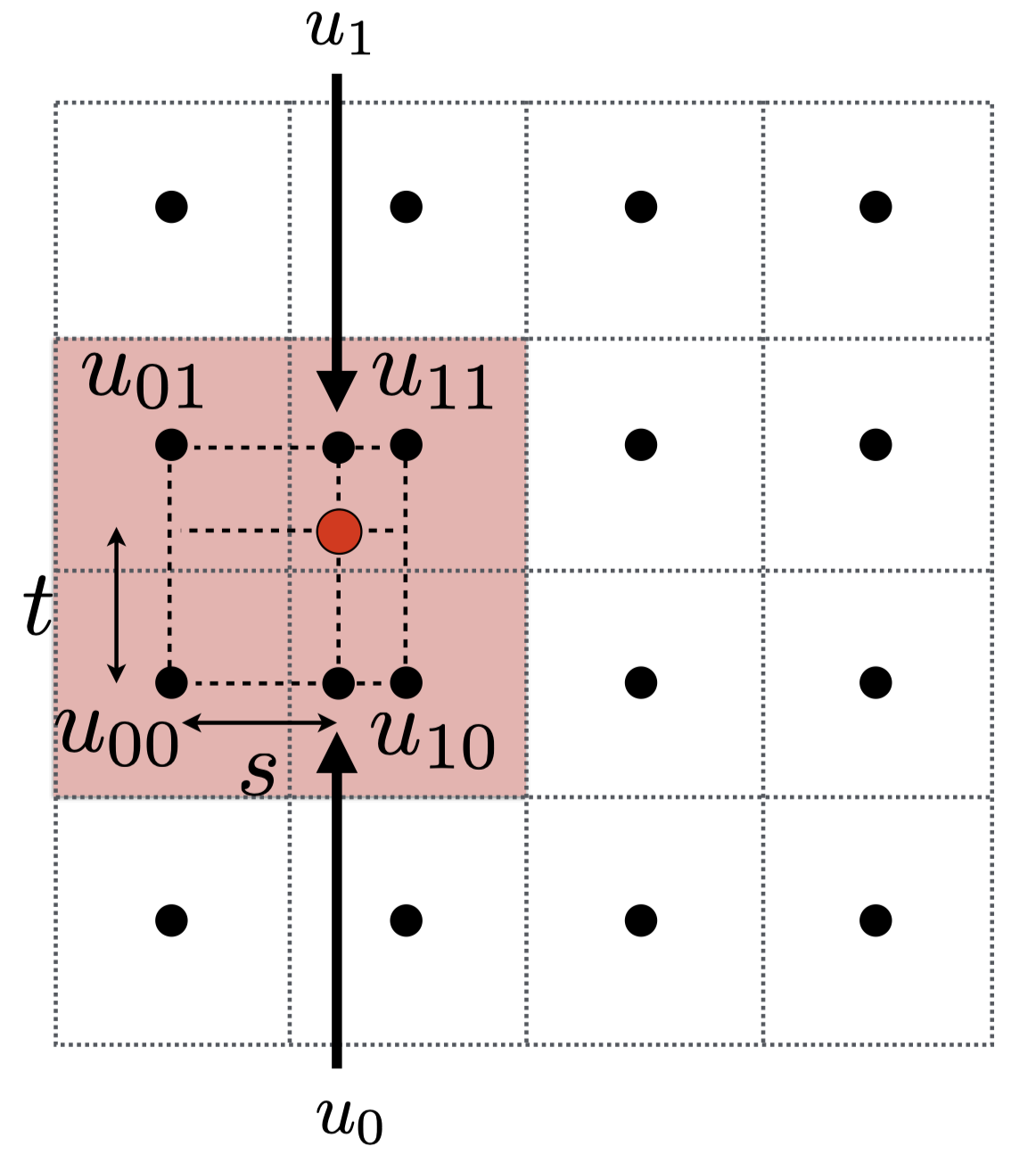 $$
f(x, y)=\operatorname{lerp}\left(t, u_0, u_1\right)
$$
$$
f(x, y)=\operatorname{lerp}\left(t, u_0, u_1\right)
$$
Mipmap
如果一个纹理过大,可能导致像素对纹理空间采样频率低,造成走样问题。如果我们不进行采样,而进行范围查询(再求平均),就可以避免这个问题。Mipmap可以提供快速、近似和对正方形内的范围查询。
Mipmap就是生成了一系列的纹理金字塔,如下所示

计算Mipmap的level的方法
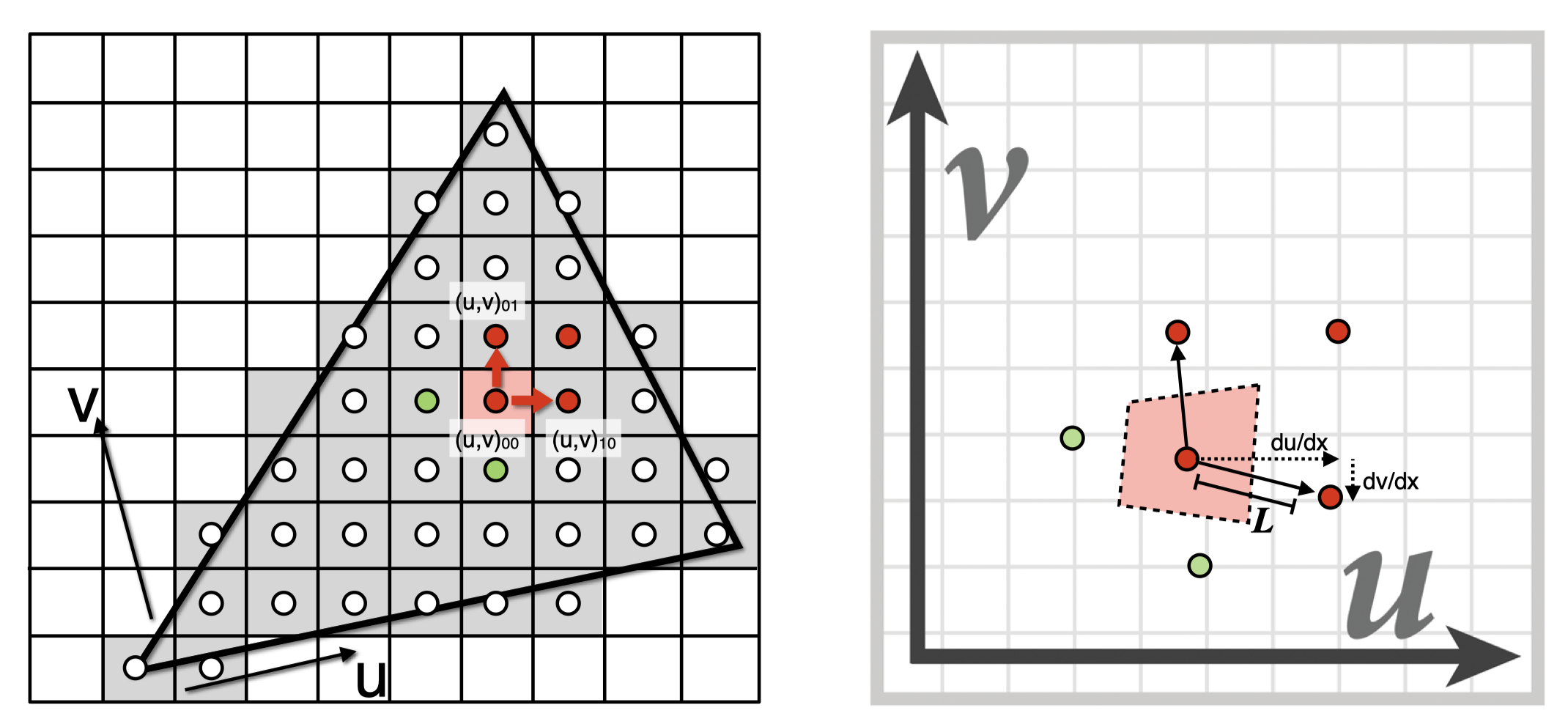 $$
\begin{aligned}
D &=\log _2 L \cr
L &=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^2+\left(\frac{d v}{d x}\right)^2}, \sqrt{\left(\frac{d u}{d y}\right)^2+\left(\frac{d v}{d y}\right)^2}\right)
\end{aligned}
$$
$$
\begin{aligned}
D &=\log _2 L \cr
L &=\max \left(\sqrt{\left(\frac{d u}{d x}\right)^2+\left(\frac{d v}{d x}\right)^2}, \sqrt{\left(\frac{d u}{d y}\right)^2+\left(\frac{d v}{d y}\right)^2}\right)
\end{aligned}
$$
各向异性过滤(Anisotropic Filtering)
可以通过各向异性过滤查找轴对齐的矩形(不仅仅是正方形)区域内的texture从而提高mipmap的效果。
环境光(Spherical Environment Map)
环境光映射是将环境光照映射到一个球上或立方体上来表示周围的环境光。
凹凸贴图(bump map)
定义uv map上某一个点沿着法线方向上高出或者低于这个平面的相对高度(在不把几何形状变复杂的情况下定义凹凸不平的表面)。凹凸贴图会改变计算shading时的法线方向。
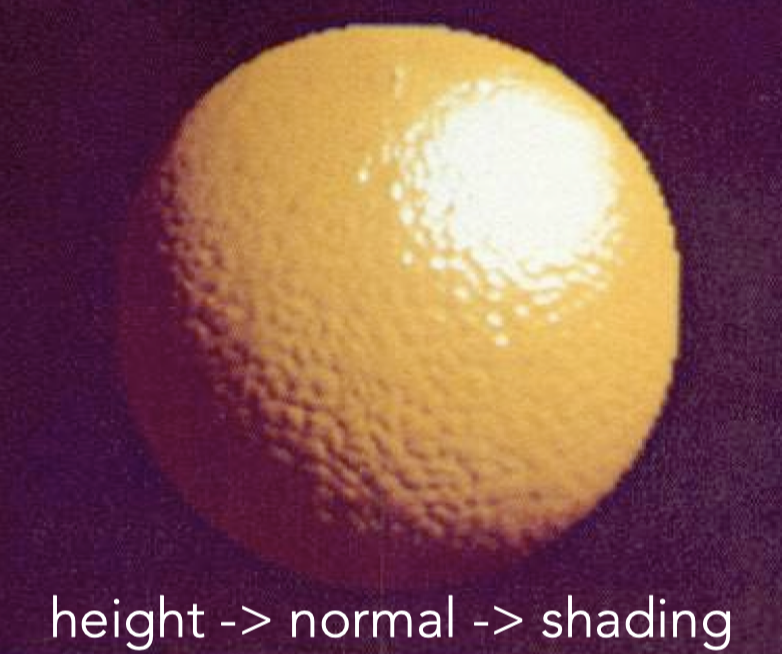
计算法线的方法: $$ \begin{aligned} & \frac{dp}{du}=c_1 *[h(\mathbf{u}+1)-h(\mathbf{u})] \cr & \frac{dp}{dv}=c_2 *[h(\mathbf{v}+1)-h(\mathbf{v})] \cr & n = (-\frac{dp}{du}, -\frac{dp}{dv}, 1).normalized() \end{aligned} $$ 其中$h$代表高度,$n$代表最后计算得到的法线。注意这个是在切线空间里计算得到的结果,最后还需要变换回原空间。
位移贴图(Displacement mapping)
位移贴图和凹凸贴图类似,都是产生凹凸的感觉,但是凹凸贴图并没有实际改变物体的几何形状,只是通过改变法线来改变shading从而造成凹凸的假象,但是位移贴图确实改变了顶点的位置。注意看下面两张图的阴影形状。
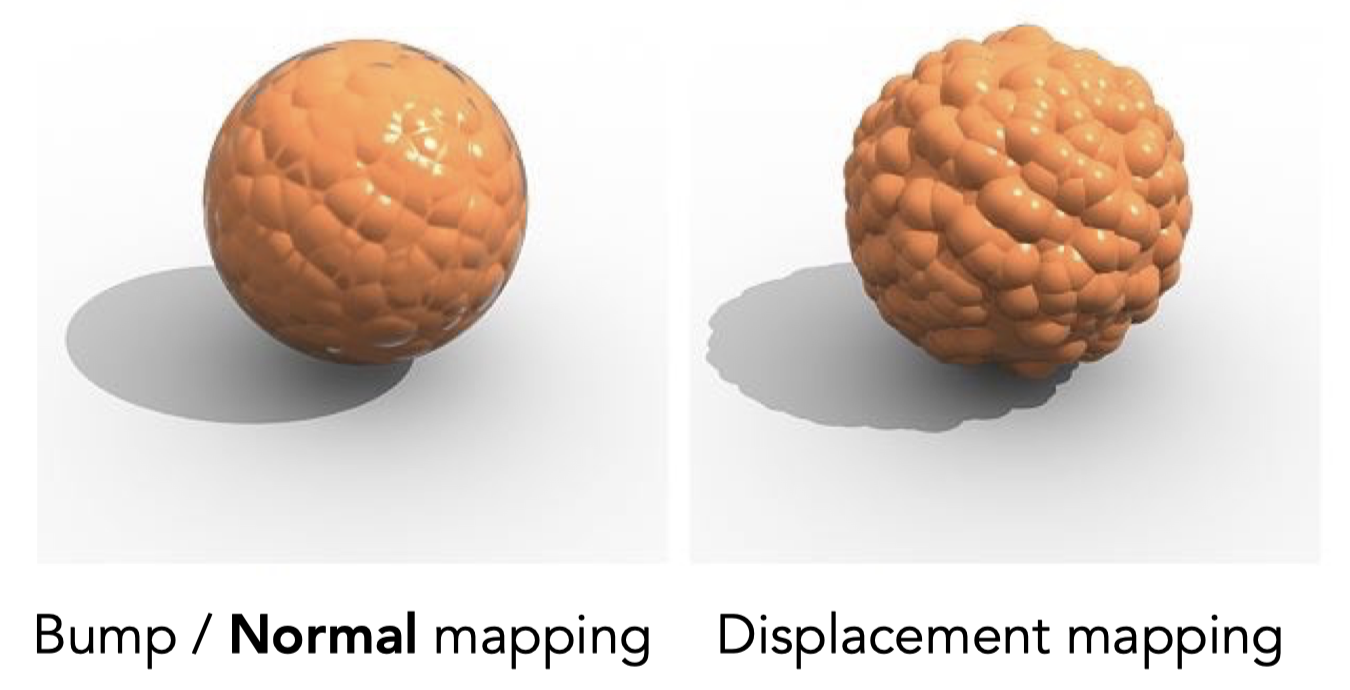
位移贴图的缺点是需要模型足够细致(三角形够小)从而跟上位移贴图的采样频率。
几何
隐式几何
所有的点满足某个数学公式所描述的关系而不直接给实际的点。隐式几何的采样比较难但是判断一个点是否在表面上比较简单。
Constructive Solid Geometry (CSG)
通过几何之间的布尔运算来组合隐式几何从而形成复杂几何
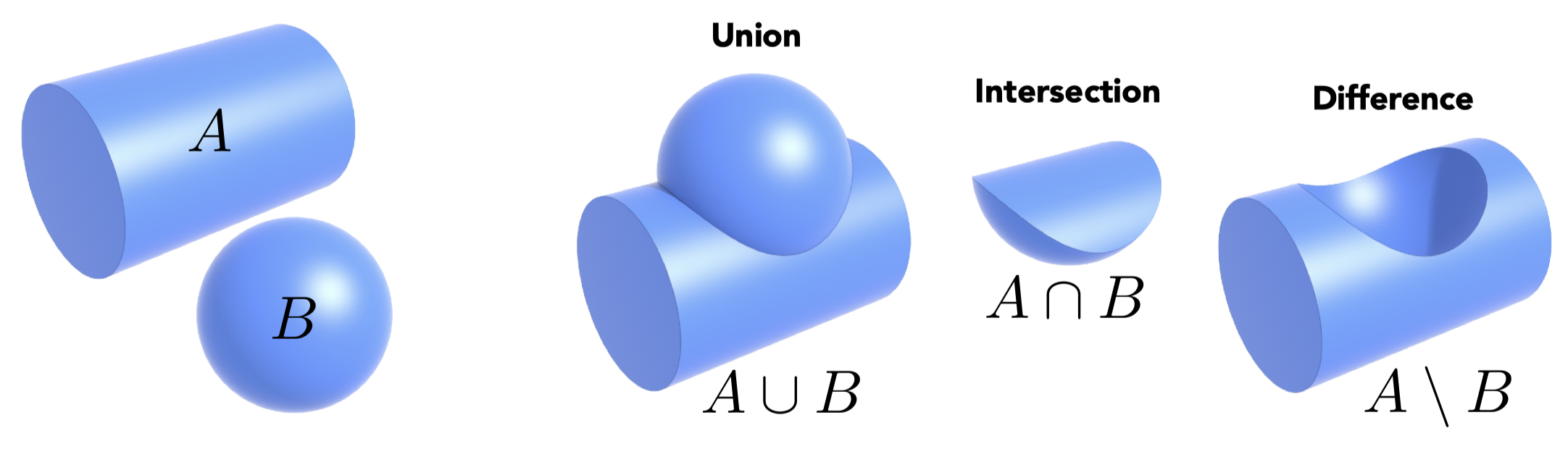
距离函数(Distance Functions)
距离函数可以用于隐式描述几何:空间中的任何一个点到几何形体上的任意一个点的最小距离(可正可负),将距离函数进行blend操作可以得到两个几何融合的边界
分形
分形也是一种隐式几何,就是几何的某一部分和整体非常相似,类似于递归的概念。分形的变化频率极高,会产生严重走样。
显式几何
直接给出所有点的坐标或者通过参数映射给出。显氏几何的采样简单但是判断一个点是否在表面上比较难。
点云
点(x, y, z)的list,常用于数据量较高的情况(> 1 point/pixel),经常被转换为多边形面(polygon mesh)
多边形面(polygon mesh)
存储顶点和多边形,多边形面组合起来形成一个物体

曲线(Curve)
贝塞尔曲线(Bézier Curve)
用一系列控制点来定义一个曲线(曲线不一定经过控制点),其中起始点的切线方向要等于起始点到下一个控制点的方向,末尾点的切线方向要等于倒数第二个控制点到末尾点的方向。下图中的蓝线就是贝塞尔曲线。
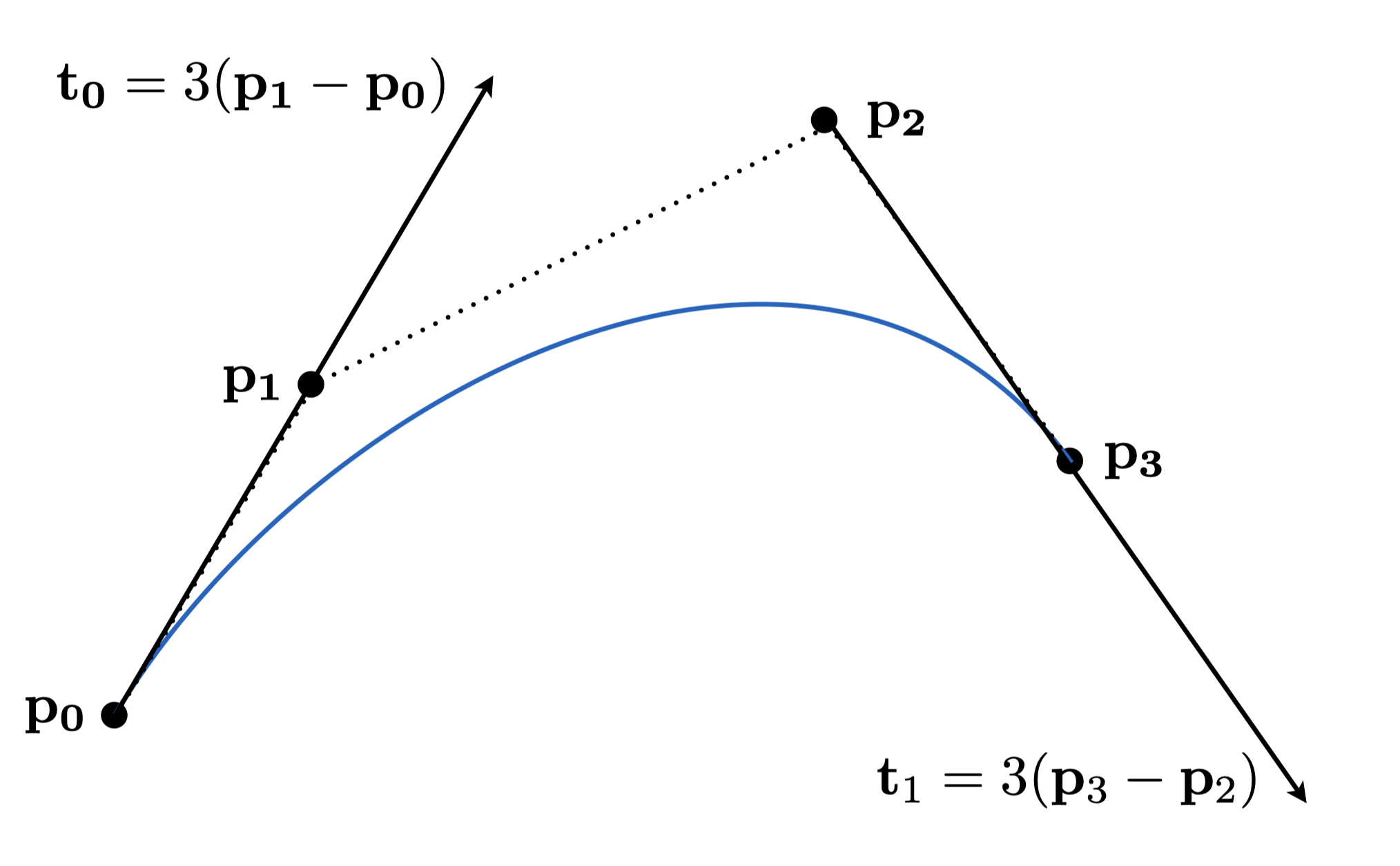
de Casteljau算法
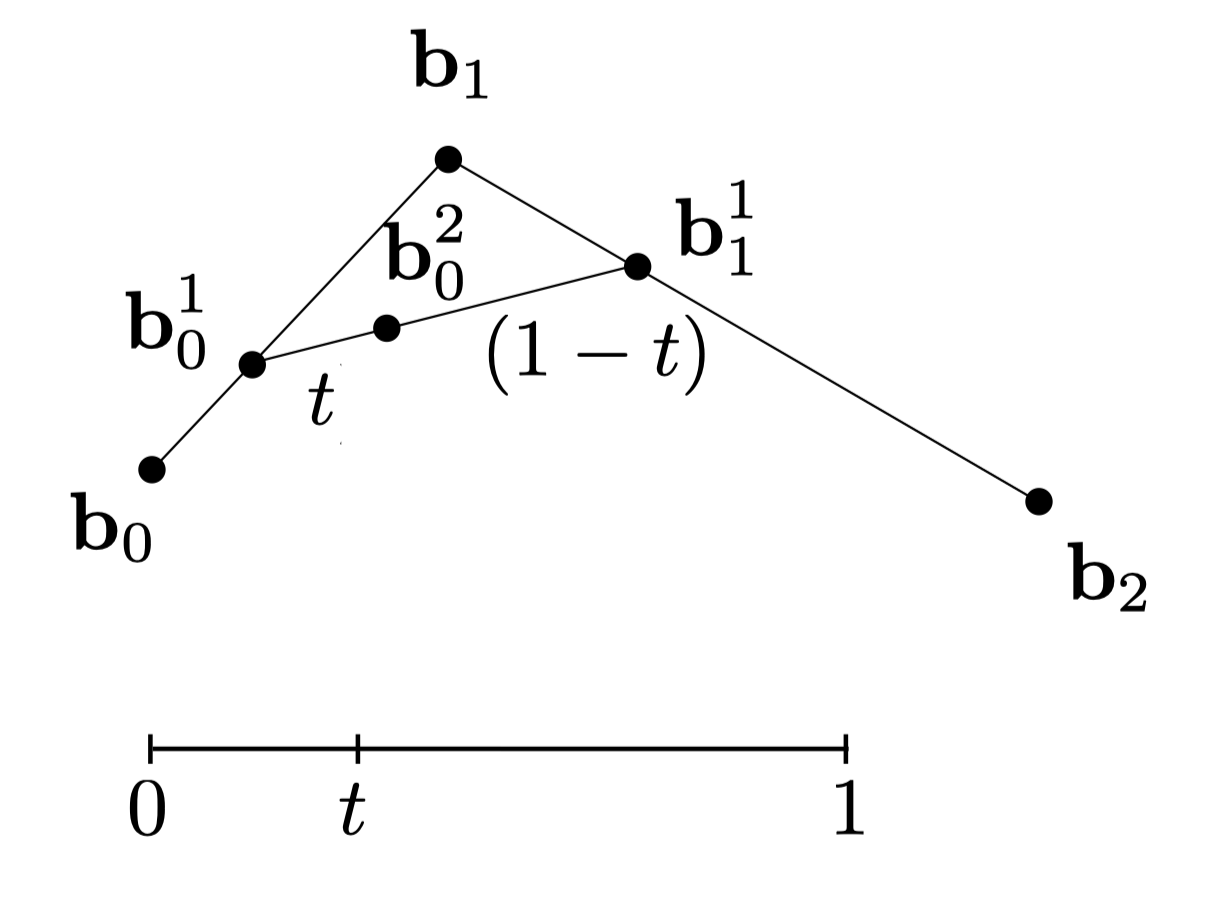
求$b_0$, $b_1$, $b_2$三个控制点形成的二阶贝塞尔曲线的方法:假设一个$[0, 1]$的时间轴,其中$b_0$点对应$t=0$的位置,$b_2$点对应$t=1$的位置,如果我们能够算出任意$t$对应的位置,我们就可以得到这个贝塞尔曲线。
做法就是分别在$b_0b_1$线段和$b_1b_2$线段上取点$b_0^1$和$b_1^1$使得$b_0b_0^1 = t \cdot b_0b_1$以及$b_1b_1^1=t\cdot b_1b_2$。然后再在$b_0^1b_1^1$上取点$b_0^2$使得$b_0^1b_0^2=t \cdot b_0^1b_1^1$。对$t$进行连续采样就可以得到贝塞尔曲线。 $$ \begin{aligned} & \mathbf{b}_0^1(t)=(1-t) \mathbf{b}_0+t \mathbf{b}_1 \cr & \mathbf{b}_1^1(t)=(1-t) \mathbf{b}_1+t \mathbf{b}_2 \cr & \mathbf{b}_0^2(t)=(1-t) \mathbf{b}_0^1+t \mathbf{b}_1^1 \cr & \mathbf{b}_0^2(t)=(1-t)^2 \mathbf{b}_0+2 t(1-t) \mathbf{b}_1+t^2 \mathbf{b}_2 \end{aligned} $$
对于更多的控制点,使用同样的递归线性插值方法。如下所示。
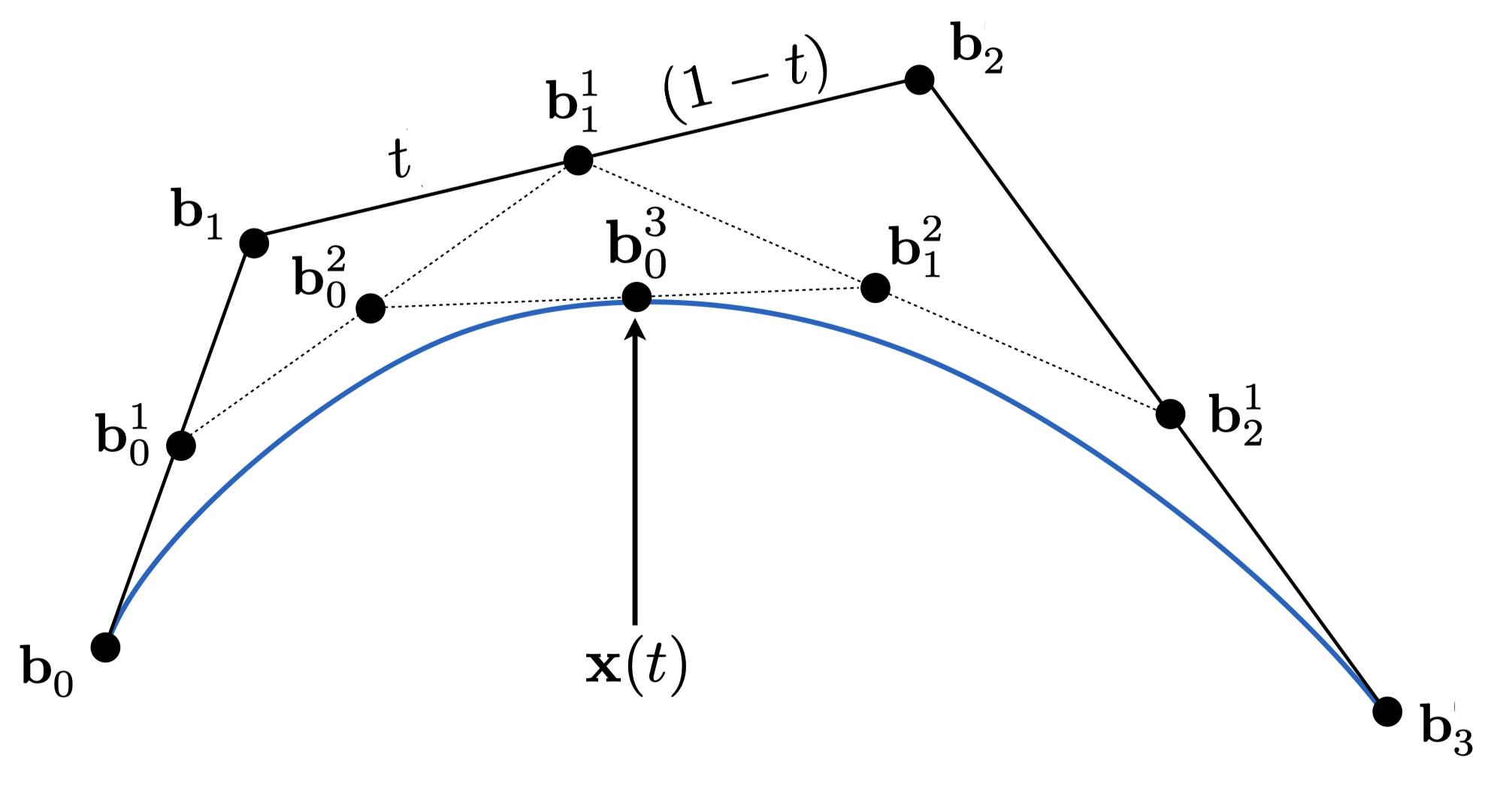
对于一个n阶贝塞尔曲线,我们使用Bernstein表达式来描述:
$$ \mathbf{b}^n(t)=\mathbf{b}0^n(t)=\sum{j=0}^n \mathbf{b}_j B_j^n(t) $$
其中$\mathbf{b}^n(t)$是n阶贝塞尔曲线在t时刻的位置,$\mathbf{b}_j$是贝塞尔控制点,$B_j^n(t)$是Bernstein多项式,由以下公式描述:
$$ B_i^n(t)=\left(\begin{array}{c} n \cr i \end{array}\right) t^i(1-t)^{n-i} $$
实际上就是二项式系数。
贝塞尔曲线的性质
- 对贝塞尔曲线控制点进行仿射变换后得到的贝塞尔曲线和对这个贝塞尔曲线上的每一个点本身进行仿射变换得到的结果相同。
- 贝塞尔曲线在所有的控制点的凸包(convex hull)内。
分段三阶贝塞尔曲线
为了方便控制曲线,很多人并不使用太高阶的贝塞尔曲线,而是使用多个三阶贝塞尔曲线连接起来成为一条曲线。为了保证连续性(C0连续和C1连续),需要保证前后两个阶段的贝塞尔曲线控制点三点一线且线段长度相等,如下所示。
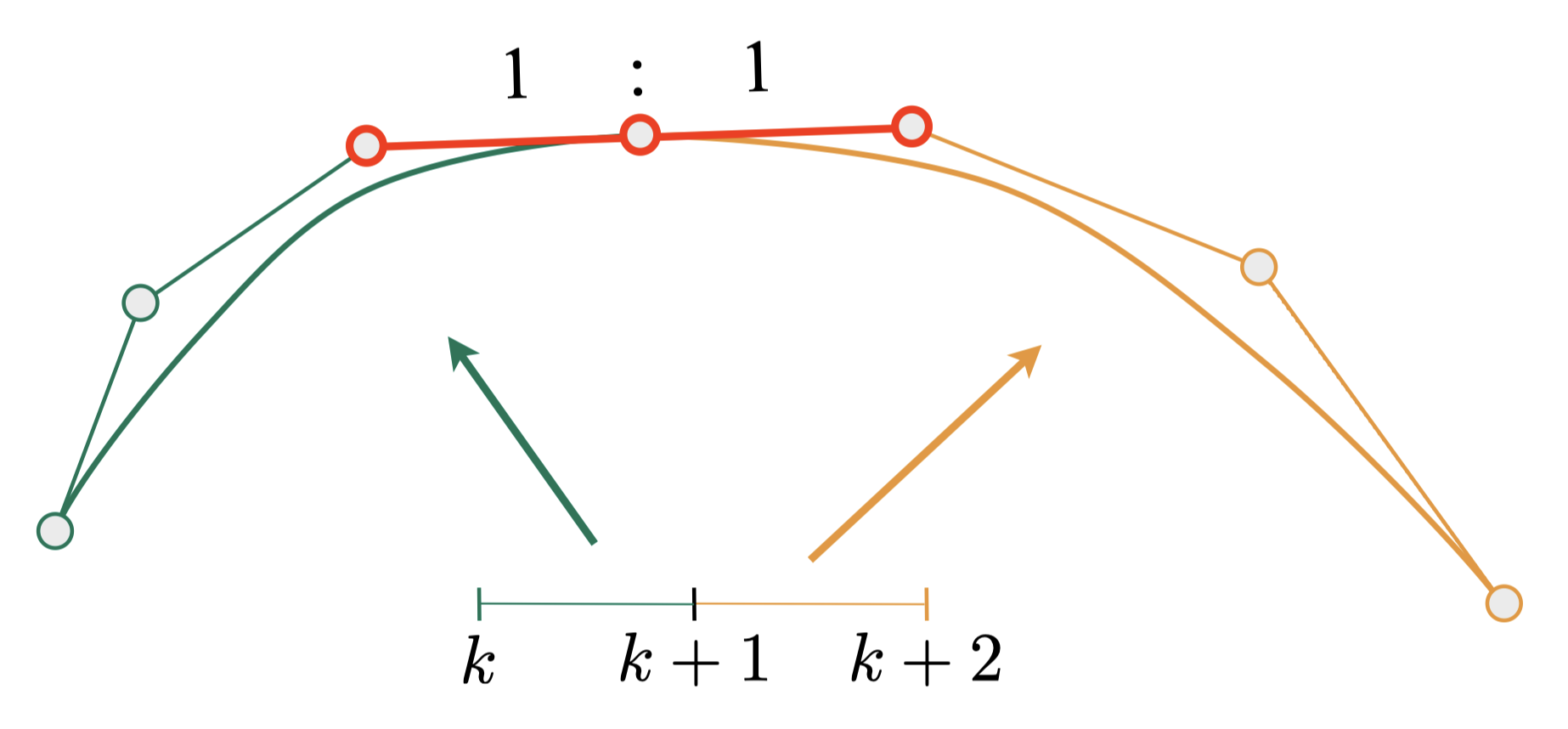
曲面(Surface)
双三次贝塞尔曲面,有一个4*4的控制点,先对每行的4个控制点得到4个三次贝塞尔曲线,然后在每一个时刻这4个贝塞尔曲线上都对应了一个点,将这4个点作为贝塞尔曲线的控制点再得到列方向上的贝塞尔曲线,t在0,1上可以得到一个移动的贝塞尔曲线,最终可以得到贝塞尔曲面。
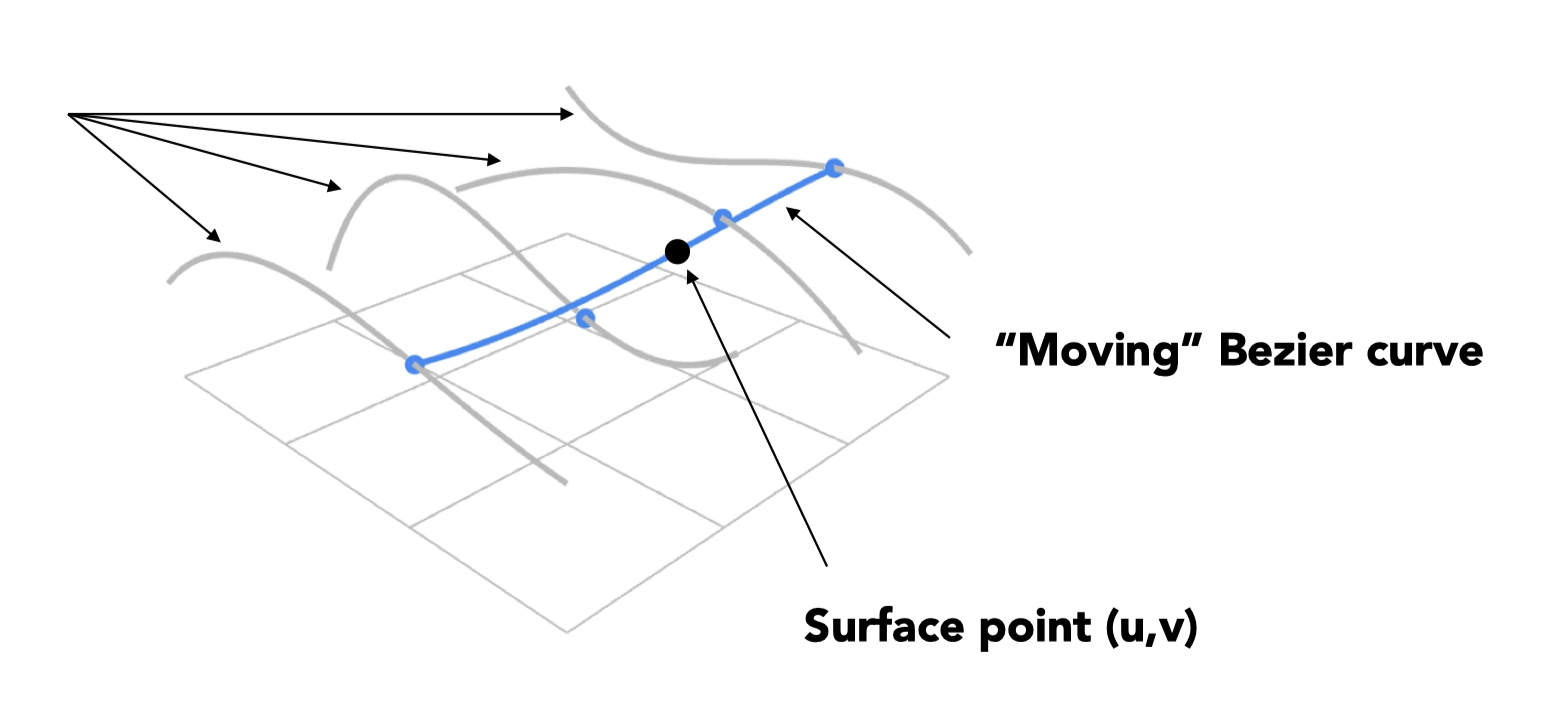
作业零
作业描述:给定一个点P=(2,1), 将该点绕原点先逆时针旋转45◦,再平移(1,2), 计算出 变换后点的坐标(要求用齐次坐标进行计算)。
#include<cmath>
#include<Eigen/Core>
#include<Eigen/Dense>
#include<iostream>
int main(){
float pi = std::acos(-1);
float alpha = 45.0f / 180.0 * pi;
Eigen::Vector3f p(2.0f, 1.0f, 1.0f);
Eigen::Matrix3f R;
R << std::cos(alpha), -std::sin(alpha), 0.0,
std::sin(alpha), std::cos(alpha), 0.0,
0.0, 0.0, 1.0;
Eigen::Matrix3f T;
T << 1.0f, 0.0f, 1.0f,
0.0f, 1.0f, 2.0f,
0.0f, 0.0f, 1.0f;
Eigen::Vector3f res = T * R * p;
std::cout << res << std::endl;
// result is 1.70711, 4.12132, 1
return 0;
}
作业一
作业描述:实现旋转矩阵和透视投影矩阵以用光栅化算法实现一个三角形
/* main.cpp */
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
// Create the model matrix for rotating the triangle around the Z axis.
// Then return it.
model(0, 0) = cos(rotation_angle * 180 / MY_PI);
model(0, 1) = -sin(rotation_angle * 180 / MY_PI);
model(1, 0) = sin(rotation_angle * 180 / MY_PI);
model(1, 1) = cos(rotation_angle * 180 / MY_PI);
return model;
}
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
float zNear, float zFar)
{
Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();
// Create the projection matrix for the given parameters.
// Then return it.
float top = tanf(eye_fov / 2.0f) * zNear;
float bottom = -top;
float right = top * aspect_ratio;
float left = -right;
projection(0, 0) = zNear / right;
projection(1, 1) = zNear / top;
projection(2, 2) = (zNear + zFar) / (zNear - zFar);
projection(2, 3) = (2 * zNear * zFar) / (zNear - zFar);
projection(3, 2) = -1.0f;
return projection;
}
实现效果:

作业二
作业描述:实现三角形的光栅化。编写
rasterize_triangle()和insideTriangle()两个函数,分别执行三角形光栅化算法和测试点是否在三角形内
rasterize_triangle()的步骤是:首先得到三角形的bounding box,即求出三角形三个顶点x,y的最大和最小值(注意这里的x和y都是在屏幕坐标内的了),然后在这个bounding box内对每个像素进行遍历,调用insideTriangle判断像素点的中心(x+0,5, y+0.5)是否在这个三角形内。然后计算插值后的z值,如果z值小于z buffer中该像素点对应的值,那么更新z buffer,并将该像素点绘制为这个三角形的颜色。
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t) {
auto v = t.toVector4();
// Find out the bounding box of current triangle.
float x_min, y_min, x_max, y_max;
x_min = y_min = std::max(width, height) + 1;
x_max = y_max = -1;
for (int i = 0; i < 3; i++) {
Vector4f vertice = v[i];
x_min = std::min(x_min, vertice.x());
y_min = std::min(y_min, vertice.y());
x_max = std::max(x_max, vertice.x());
y_max = std::max(y_max, vertice.y());
}
// iterate through the pixel and find if the current pixel is inside the triangle
for (int i = (int) x_min; i <= (int) x_max; i++) {
for (int j = (int) y_min; j <= (int) y_max; j++) {
if (insideTriangle(i, j, t.v)) {
int idx = get_index(i, j);
// get the interpolated z value
auto[alpha, beta, gamma] = computeBarycentric2D(i + 0.5, j + 0.5, t.v);
float w_reciprocal = 1.0/(alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
if (z_interpolated < depth_buf[idx]) {
depth_buf[idx] = z_interpolated;
// set the current pixel to the color of the triangle if it should be painted.
set_pixel(Vector3f(i, j, 0.0), t.getColor());
}
}
}
}
}
insideTriangle()非常简单,利用光栅化2D采样中最后提到的叉乘方法即可
static bool insideTriangle(int x, int y, const Vector3f* _v)
{
float x_pos = x + 0.5f;
float y_pos = y + 0.5f;
Vector3f QP0 = Vector3f(_v[0].x() - x_pos, _v[0].y() - y_pos, 0.0);
Vector3f QP1 = Vector3f(_v[1].x() - x_pos, _v[1].y() - y_pos, 0.0);
Vector3f QP2 = Vector3f(_v[2].x() - x_pos, _v[2].y() - y_pos, 0.0);
Vector3f P0P1 = Vector3f(_v[1].x() - _v[0].x(), _v[1].y() - _v[0].y(), 0.0);
Vector3f P1P2 = Vector3f(_v[2].x() - _v[1].x(), _v[2].y() - _v[1].y(), 0.0);
Vector3f P2P0 = Vector3f(_v[0].x() - _v[2].x(), _v[0].y() - _v[2].y(), 0.0);
float res1 = QP0.cross(P0P1).z();
float res2 = QP1.cross(P1P2).z();
float res3 = QP2.cross(P2P0).z();
return (res1 >= 0.0 && res2 >= 0.0 && res3 >= 0.0) || (res1 <= 0.0 && res2 <= 0.0 && res3 <= 0.0);
}
最后得到的结果如下所示:
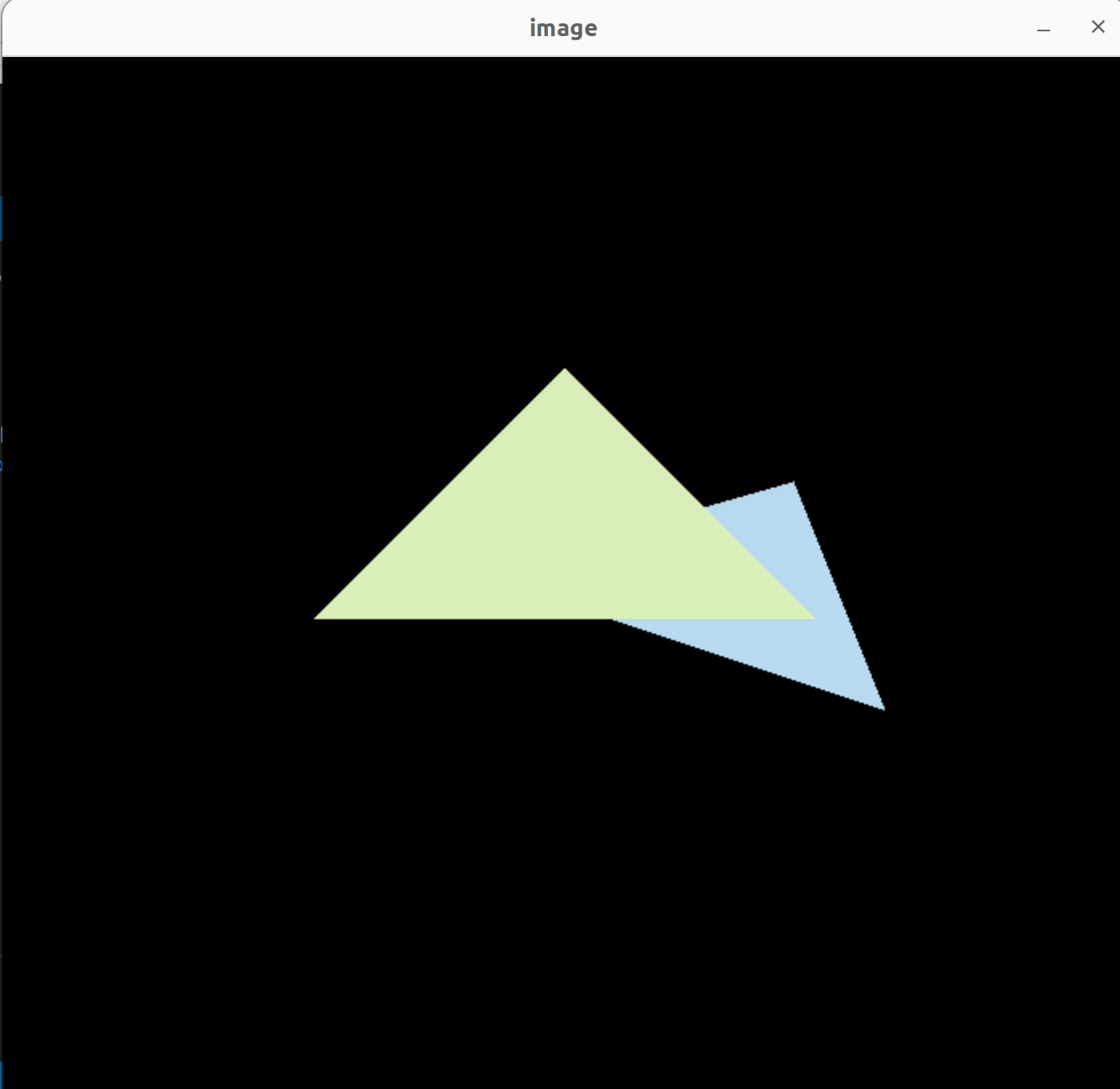
作业三
本次作业内容较多,需要完成的任务主要是实现blinn-phong光照模型的着色算法,并根据不同的纹理渲染模型。
修改函数
rasterize_triangle(const Triangle& t)in rasterizer.cpp,实现与作业二类似的插值算法,实现法向量、颜色、纹理颜色的插值。
在这里我们需要先计算重心坐标,得到$\alpha$,$\beta$,$\gamma$后并不能直接将顶点上的属性值代入,而是需要经过投影校正之后计算相应属性的插值。
注意,我们需要计算interpolated_shadingcoords将插值位置的点变换回相机坐标下的位置,从而在blinn-phong模型中计算漫反射和高光时提供正确的$r$。这里经过透视变换后得到的$w$分量实际上应该是摄像机坐标系下的深度位置(透视投影变换矩阵最后一行为$0, 0, -1, 0$),但是这里代码框架实际上是有问题的,因为经过auto v = t.toVector4()之后$w$分量被强制写为了1。
得到插值后的属性后将属性作为payload代入fragment_shader即可得到这个像素下的正确颜色。代码如下所示:
//Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle& t, const std::array<Eigen::Vector3f, 3>& view_pos)
{
auto v = t.toVector4();
// Find out the bounding box of current triangle.
float x_min, y_min, x_max, y_max;
x_min = y_min = std::max(width, height) + 1;
x_max = y_max = -1;
for (int i = 0; i < 3; i++) {
Vector4f vertice = v[i];
x_min = std::min(x_min, vertice.x());
y_min = std::min(y_min, vertice.y());
x_max = std::max(x_max, vertice.x());
y_max = std::max(y_max, vertice.y());
}
// iterate through the pixel and find if the current pixel is inside the triangle
for (int i = (int) x_min; i <= (int) x_max; i++) {
for (int j = (int) y_min; j <= (int) y_max; j++) {
if (insideTriangle(i, j, t.v)) {
int idx = get_index(i, j);
// get the interpolated z value
auto[alpha, beta, gamma] = computeBarycentric2D(i + 0.5, j + 0.5, t.v);
// * v[i].w() is the vertex view space depth value z.
// * Z is interpolated view space depth for the current pixel
// * zp is depth between zNear and zFar, used for z-buffer
// projection interpolation adjust
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float zp = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
zp *= Z;
if (zp < depth_buf[idx]) {
depth_buf[idx] = zp;
// interpolate the attributes for shader
Vector3f interpolated_color = interpolate(alpha, beta, gamma, t.color[0], t.color[1], t.color[2], 1.0);
Vector3f interpolated_normal = interpolate(alpha, beta, gamma, t.normal[0], t.normal[1], t.normal[2], 1.0);
Vector2f interpolated_texcoords = interpolate(alpha, beta, gamma, t.tex_coords[0], t.tex_coords[1], t.tex_coords[2], 1.0);
// shading coords is to find the corresponding position of the shading point in the real world space in order to be used in the blinn-phong model
Vector3f interpolated_shadingcoords = interpolate(alpha, beta, gamma, view_pos[0], view_pos[1], view_pos[2], 1.0);
// generate a shader payload
auto payload = fragment_shader_payload(interpolated_color, interpolated_normal.normalized(), interpolated_texcoords, texture ? &*texture : nullptr);
payload.view_pos = interpolated_shadingcoords;
auto pixel_color = fragment_shader(payload);
set_pixel(Vector2i(i, j), pixel_color);
}
}
}
}
}
得到的法线贴图结果为

修改函数
phong_fragment_shader()in main.cpp,实现Blinn-Phong模型计算fragment color
直接套用Blinn-phong模型公式即可。注意$\mathbf{l}$、$\mathbf{n}$、$\mathbf{r}$等需要进行归一化处理。
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// parameters to use
Vector3f l = (light.position - point).normalized();
Vector3f v = (eye_pos - point).normalized();
Vector3f h = (v + l).normalized();
float r_square = (light.position - point).dot(light.position - point);
// ambient light
Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
// diffusion light
Vector3f diffusion = kd.cwiseProduct(light.intensity / r_square) * std::max(0.0f, normal.normalized().dot(l.normalized()));
// specular light
Vector3f specular = ks.cwiseProduct(light.intensity / r_square) * pow((std::max(0.0f, normal.normalized().dot(h))), p);
result_color += (ambient + diffusion + specular);
}
return result_color * 255.f;
}
得到的渲染结果,注意高光的位置:

修改函数
texture_fragment_shader()in main.cpp,在实现Blinn-Phong的基础上,将纹理颜色视为公式中的kd,实现texture shading fragment shader
非常简单,只需要通过payload.texture->getColor求对应纹理贴图纹素的颜色代入$kd$即可。
Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f return_color = {0, 0, 0};
if (payload.texture)
{
// Get the texture value at the texture coordinates of the current fragment
return_color = payload.texture->getColor(payload.tex_coords.x(), payload.tex_coords.y());
}
Eigen::Vector3f texture_color;
texture_color << return_color.x(), return_color.y(), return_color.z();
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = texture_color / 255.f;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = texture_color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// parameters to use
Vector3f l = (light.position - point).normalized();
Vector3f v = (eye_pos - point).normalized();
Vector3f h = (v + l).normalized();
float r_square = (light.position - point).dot(light.position - point);
// ambient light
Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
// diffusion light
Vector3f diffusion = kd.cwiseProduct(light.intensity / r_square) * std::max(0.0f, normal.normalized().dot(l.normalized()));
// specular light
Vector3f specular = ks.cwiseProduct(light.intensity / r_square) * pow((std::max(0.0f, normal.normalized().dot(h))), p);
result_color += (ambient + diffusion + specular);
}
return result_color * 255.f;
}
注意OpenCV 4.xx版本可能会在运行时产生segmentation fault,这是由于texture.hpp中的getColor有数组越界的问题,需要进行如下修改:
Eigen::Vector3f getColor(float u, float v)
{
// add this line
if (u <= 0 || u >= 1 || v <= 0 || v >= 1) {
return Eigen::Vector3f(0, 0, 0);
}
auto u_img = u * width;
auto v_img = (1 - v) * height;
auto color = image_data.at<cv::Vec3b>(v_img, u_img);
return Eigen::Vector3f(color[0], color[1], color[2]);
}
实现的渲染效果:

修改函数
bump_fragment_shader()in main.cpp,实现凹凸贴图
这里主要难点在于切线空间的转化,使用了TBN矩阵进行变换将计算得到的切线空间坐标法线变换为世界空间坐标,这一部分可以参考https://zhuanlan.zhihu.com/p/412555049进行理解。同时我们这里的高度场使用了payload.texture->getColor().norm()来进行计算。最终的代码如下所示:
Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// Implement bump mapping
// Let n = normal = (x, y, z)
Vector3f n = normal;
Vector3f t = Vector3f(n.x() * n.y() / std::sqrt(n.x() * n.x() + n.z() * n.z()), std::sqrt(n.x() * n.x() + n.z() * n.z()), n.z() * n.y() / std::sqrt(n.x() * n.x() + n.z() * n.z()));
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0 / w, v) .norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln = Vector3f(-dU, -dV, 1.0f);
n = (TBN * ln).normalized();
Eigen::Vector3f result_color = {0, 0, 0};
result_color = n;
return result_color * 255.f;
}
最终效果如下所示

修改函数displacement_fragment_shader() 实现位移贴图
位移贴图和凹凸贴图类似,唯一的区别就是需要修改point
Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload& payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
Vector3f n = normal;
Vector3f t = Vector3f(n.x() * n.y() / std::sqrt(n.x() * n.x() + n.z() * n.z()), std::sqrt(n.x() * n.x() + n.z() * n.z()), n.z() * n.y() / std::sqrt(n.x() * n.x() + n.z() * n.z()));
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), normal.x(),
t.y(), b.y(), normal.y(),
t.z(), b.z(), normal.z();
float u = payload.tex_coords.x();
float v = payload.tex_coords.y();
float w = payload.texture->width;
float h = payload.texture->height;
float dU = kh * kn * (payload.texture->getColor(u + 1.0 / w, v) .norm() - payload.texture->getColor(u, v).norm());
float dV = kh * kn * (payload.texture->getColor(u, v + 1.0 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln = Vector3f(-dU, -dV, 1.0f);
n = (TBN * ln).normalized();
// change position of point according to the displacement map
point += kn * n * payload.texture->getColor(u, v).norm();
Eigen::Vector3f result_color = {0, 0, 0};
for (auto& light : lights)
{
// parameters to use
Vector3f l = (light.position - point).normalized();
Vector3f v = (eye_pos - point).normalized();
Vector3f h = (v + l).normalized();
float r_square = (light.position - point).dot(light.position - point);
// ambient light
Vector3f ambient = ka.cwiseProduct(amb_light_intensity);
// diffusion light
Vector3f diffusion = kd.cwiseProduct(light.intensity / r_square) * std::max(0.0f, normal.normalized().dot(l.normalized()));
// specular light
Vector3f specular = ks.cwiseProduct(light.intensity / r_square) * pow((std::max(0.0f, normal.normalized().dot(h))), p);
result_color += (ambient + diffusion + specular);
}
return result_color * 255.f;
}
实现的效果如下:
