Fenwick Tree

树状数组, 英文Fenwick Tree或Binary Index Tree, 是一种用来在$O(\log N)$时间复杂度内进行前缀和更新和查找的数据结构

Leetcode 307. Range Sum Query - Mutable

问题

Given an integer array nums, handle multiple queries of the following types:

1. Update the value of an element in nums.
2. Calculate the sum of the elements of nums between indices left and right inclusive where left <= right.

Implement the NumArray class:

• NumArray(int[] nums) Initializes the object with the integer array nums.
• void update(int index, int val) Updates the value of nums[index] to be val.
• int sumRange(int left, int right) Returns the sum of the elements of nums between indices left and right inclusive(i.e. nums[left] + nums[left + 1] + ... + nums[right]).

示例

Input
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
Output
[null, 9, null, 8]

Explanation
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // return 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1, 2, 5]
numArray.sumRange(0, 2); // return 1 + 2 + 5 = 8

限制条件

• 1 <= nums.length <= 3 * 10^4
• -100 <= nums[i] <= 100
• 0 <= index < nums.length
• -100 <= val <= 100
• 0 <= left <= right < nums.length
• At most 3 * 10^4 calls will be made to update and sumRange.

题解

树状数组是线段树的一种特例，比线段树更为简单，但是只能求解特定的区间查询问题（前缀和问题）。

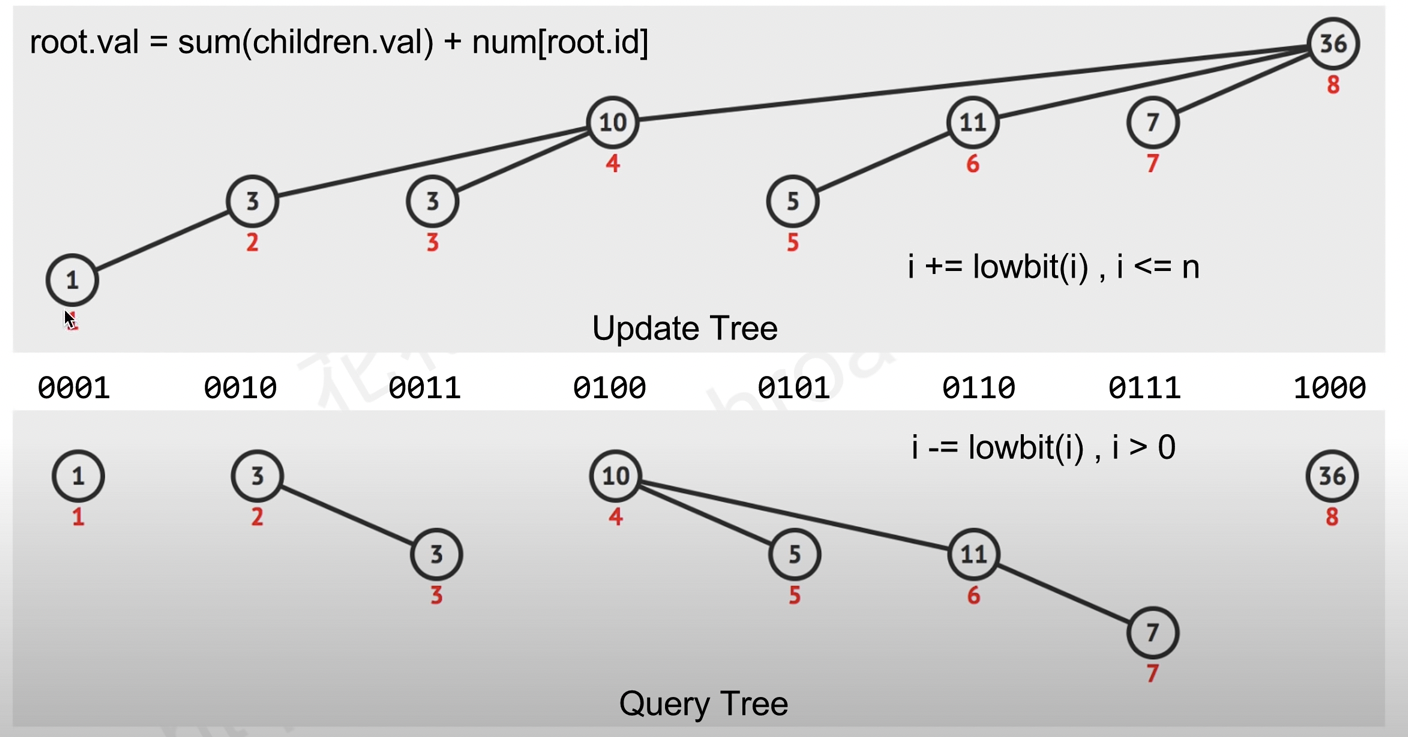
如上图所示，树状数组分为更新和查询两个步骤，并维护一个长度为n的sum数组(1-indexed)，并假设原数组为num。我们可以得到以下映射关系：sum[1] = num[1], sum[2] = num[1] + num[2], sum[3] = num[3], sum[4] = num[1] + num[2] + num[3] + num[4], sum[5] = num[5], sum[6] = num[5] + num[6], sum[7] = num[7], sum[8] = num[1] + num[2] + num[3] + num[4] + num[5] + num[6] + num[7] + num[8]， 以此类推，即当$$n = 2^k$$时$$sum[n] = sum(num[1:n])$$。可以理解为lowest bit 1越高，这个数在树中的层级越高，一个sum[10000](sum[16])就是由sum[1000] + sum[1100] + sum[1110] + sum[1111]组成，可以看到lowest bit 1越来越低。

Lowest bit 1快速的获取方法是x & (-x)。

代码如下：

def lowbit(x):
    return x & (-x)

## Binary Index Tree
class BIT:
    def __init__(self, nums):
        self.nums = nums
        self.sums = [0 for _ in range(len(nums) + 1)]

    def update(self, i, delta):
        while i <= len(self.nums):
            self.sums[i] += delta
            i += lowbit(i)

    def query(self, i):
        res = 0
        while i > 0:
            res += self.sums[i]
            i -= lowbit(i)
        return res

class NumArray: 
    def __init__(self, nums: List[int]):
        self.bit = BIT(nums)
        self.nums = nums
        for i in range(1, len(nums) + 1):
            self.bit.update(i, nums[i - 1])
        

    def update(self, index: int, val: int) -> None:
        self.bit.update(index + 1, val - self.nums[index])
        self.nums[index] = val

    def sumRange(self, left: int, right: int) -> int:
        return self.bit.query(right + 1) - self.bit.query(left)
    

# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# obj.update(index,val)
# param_2 = obj.sumRange(left,right)