Trie Problem
本文讨论可以使用前缀树Trie来解决的一些问题。
Leetcode 1948. 删除系统中的重复文件夹
问题
由于一个漏洞,文件系统中存在许多重复文件夹。给你一个二维数组paths,其中paths[i]是一个表示文件系统中第i个文件夹的绝对路径的数组。
- 例如,[“one”, “two”, “three”] 表示路径 “/one/two/three” 。
如果两个文件夹(不需要在同一层级)包含 非空且相同的 子文件夹 集合 并具有相同的子文件夹结构,则认为这两个文件夹是相同文件夹。相同文件夹的根层级 不 需要相同。如果存在两个(或两个以上)相同 文件夹,则需要将这些文件夹和所有它们的子文件夹 标记 为待删除。
- 例如,下面文件结构中的文件夹 “/a” 和 “/b” 相同。它们(以及它们的子文件夹)应该被 全部 标记为待删除: /a /a/x /a/x/y /a/z /b /b/x /b/x/y /b/z
然而,如果文件结构中还包含路径 “/b/w” ,那么文件夹 “/a” 和 “/b” 就不相同。注意,即便添加了新的文件夹 “/b/w” ,仍然认为 “/a/x” 和 “/b/x” 相同。 一旦所有的相同文件夹和它们的子文件夹都被标记为待删除,文件系统将会 删除 所有上述文件夹。文件系统只会执行一次删除操作。执行完这一次删除操作后,不会删除新出现的相同文件夹。
返回二维数组ans,该数组包含删除所有标记文件夹之后剩余文件夹的路径。路径可以按 任意顺序 返回。
示例
示例 1:
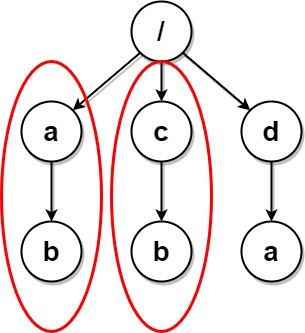
输入:paths = [["a"],["c"],["d"],["a","b"],["c","b"],["d","a"]]
输出:[["d"],["d","a"]]
解释:文件结构如上所示。
文件夹 "/a" 和 "/c"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "b" 的空文件夹。
示例 2:
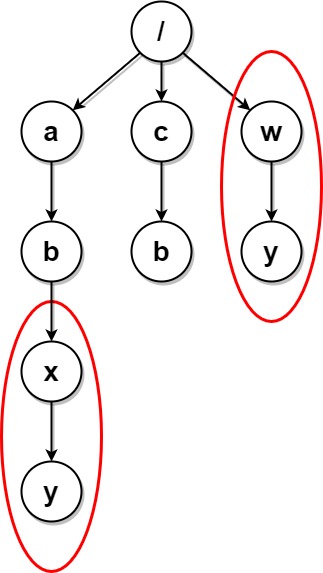
输入:paths = [["a"],["c"],["a","b"],["c","b"],["a","b","x"],["a","b","x","y"],["w"],["w","y"]]
输出:[["c"],["c","b"],["a"],["a","b"]]
解释:文件结构如上所示。
文件夹 "/a/b/x" 和 "/w"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
注意,文件夹 "/a" 和 "/c" 在删除后变为相同文件夹,但这两个文件夹不会被删除,因为删除只会进行一次,且它们没有在删除前被标记。
示例 3:
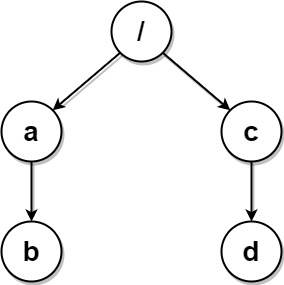
输入:paths = [["a","b"],["c","d"],["c"],["a"]]
输出:[["c"],["c","d"],["a"],["a","b"]]
解释:文件系统中所有文件夹互不相同。
注意,返回的数组可以按不同顺序返回文件夹路径,因为题目对顺序没有要求。
示例 4:
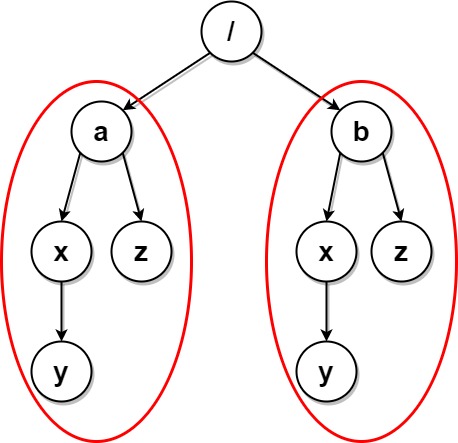
输入:paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"]]
输出:[]
解释:文件结构如上所示。
文件夹 "/a/x" 和 "/b/x"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含名为 "y" 的空文件夹。
文件夹 "/a" 和 "/b"(以及它们的子文件夹)都会被标记为待删除,因为它们都包含一个名为 "z" 的空文件夹以及上面提到的文件夹 "x" 。
示例 5:
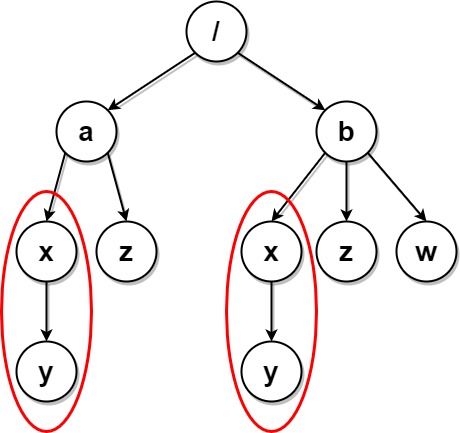
输入:paths = [["a"],["a","x"],["a","x","y"],["a","z"],["b"],["b","x"],["b","x","y"],["b","z"],["b","w"]]
输出:[["b"],["b","w"],["b","z"],["a"],["a","z"]]
解释:本例与上例的结构基本相同,除了新增 "/b/w" 文件夹。
文件夹 "/a/x" 和 "/b/x" 仍然会被标记,但 "/a" 和 "/b" 不再被标记,因为 "/b" 中有名为 "w" 的空文件夹而 "/a" 没有。
注意,"/a/z" 和 "/b/z" 不会被标记,因为相同子文件夹的集合必须是非空集合,但这两个文件夹都是空的。
限制条件
1 <= paths.length <= 2 * 10^4
1 <= paths[i].length <= 500
1 <= paths[i][j].length <= 10
1 <= sum(paths[i][j].length) <= 2 * 10^5 path[i][j] 由小写英文字母组成,不会存在两个路径都指向同一个文件夹的情况,对于不在根层级的任意文件夹,其父文件夹也会包含在输入中
题解
这道题首先需要用前缀树来建一个多叉树,因此需要自定义一个前缀树节点类,用一个map来建立字符串到子节点node之间的映射关系。
// 前缀树节点
private class Node {
TreeMap<String, Node> nextMap; // 记录下面的所有节点
boolean mark; // 标记是否需要被删除
public Node() {
this.nextMap = new TreeMap<>();
this.mark = false;
}
public boolean equals(Node node) {
// 判断当前节点下面结构中的文件夹是否相等
if (!nextMap.keySet().equals(node.nextMap.keySet())) {
return false;
}
for (Map.Entry<String, Node> entry : nextMap.entrySet()) {
if (!entry.getValue().equals(node.nextMap.get(entry.getKey()))) {
return false;
}
}
return true;
}
}
前缀树构建完成后,需要进行递归来将每个node下面的结构进行哈希存储到哈希表中,但是要注意,对象的哈希很可能产生哈希碰撞,因此hash值相同的2个node结构不一定完全一致,因此在Node类中还需要用一个equals来递归地判断子结构。如果发现当前node的结构确实已经出现过了,那么标记这个node
最后用DFS递归地删除被标记的节点
class Solution {
public List<List<String>> deleteDuplicateFolder(List<List<String>> paths) {
List<List<String>> ret = new ArrayList<>();
// 构建前缀树
Node root = new Node();
for (List<String> path : paths) {
Node node = root; // 从root开始
for (String s : path) {
node = node.nextMap.computeIfAbsent(s, t -> new Node());
}
}
// 回溯判断相同结构
dfs(root, new HashMap<>());
// 递归删除所有标记为true的节点和子树
delete(root, new ArrayList<>(), ret);
return ret;
}
// 对前缀树的节点进行hash,采用后序遍历
private int dfs(Node root, HashMap<Integer, ArrayList<Node>> map) {
int hash = 1;
for (Map.Entry<String, Node> entry : root.nextMap.entrySet()) {
hash = Objects.hash(hash, entry.getKey(), dfs(entry.getValue(), map));
}
// 标记拥有相同hash值的节点
if (!root.nextMap.isEmpty()) {
for (Node node : map.getOrDefault(hash, new ArrayList<>())) {
// 注意:这里可能产生哈希碰撞,因此要用Node中的equals来判断一下到底是不是相同的结构
if (root.equals(node)) {
root.mark = node.mark = true;
break;
}
}
}
map.computeIfAbsent(hash, t -> new ArrayList<>()).add(root);
return hash;
}
private void delete(Node root, ArrayList<String> path, List<List<String>> ret) {
// 删除所有标记为true的节点
if (!root.mark) {
if (!path.isEmpty()) {
ret.add(new ArrayList<>(path));
}
for (Map.Entry<String, Node> entry : root.nextMap.entrySet()) {
path.add(entry.getKey());
delete(entry.getValue(), path, ret);
path.remove(path.size() - 1);
}
}
}
// 前缀树节点
private class Node {
TreeMap<String, Node> nextMap; // 记录下面的所有节点
boolean mark; // 标记是否需要被删除
public Node() {
this.nextMap = new TreeMap<>();
this.mark = false;
}
public boolean equals(Node node) {
// 判断当前节点下面结构中的文件夹是否相等
if (!nextMap.keySet().equals(node.nextMap.keySet())) {
return false;
}
for (Map.Entry<String, Node> entry : nextMap.entrySet()) {
if (!entry.getValue().equals(node.nextMap.get(entry.getKey()))) {
return false;
}
}
return true;
}
}
}
Leetcode 1707. 与数组中元素的最大异或值
问题
给你一个由非负整数组成的数组nums。另有一个查询数组queries,其中queries[i] = [xi, mi]。
第i个查询的答案是xi和任何nums数组中不超过mi的元素按位异或(XOR)得到的最大值。换句话说,答案是max(nums[j] XOR xi) ,其中所有j均满足nums[j] <= mi。如果nums中的所有元素都大于mi,最终答案就是 -1 。
返回一个整数数组answer作为查询的答案,其中answer.length == queries.length且answer[i]是第i个查询的答案。
示例
示例 1:
输入:nums = [0,1,2,3,4], queries = [[3,1],[1,3],[5,6]]
输出:[3,3,7]
解释:
1) 0 和 1 是仅有的两个不超过 1 的整数。0 XOR 3 = 3 而 1 XOR 3 = 2 。二者中的更大值是 3 。
2) 1 XOR 2 = 3.
3) 5 XOR 2 = 7.
示例 2:
输入:nums = [5,2,4,6,6,3], queries = [[12,4],[8,1],[6,3]]
输出:[15,-1,5]
限制条件
1 <= nums.length, queries.length <= 10^5
queries[i].length == 2
0 <= nums[j], xi, mi <= 10^9
题解
这道题可以用前缀树Trie来进行解决。首先我们考虑如果去掉mi的限制,如何解决这个问题。可以将nums中的每个元素都看作是一个长度为31的二进制串,按照高位在上层低位在下层的顺序形成一个前缀树,如下图所示
要求最大的异或值,就需要在每一层的节点寻找和输入值对应的位相反的哪一个节点,比如输入值最高位为1,那么我们需要寻找root的0节点,如果没有这个0节点才去找1节点,这样遍历下来的节点所表示的那个值再和输入值进行异或就是最大的异或值。
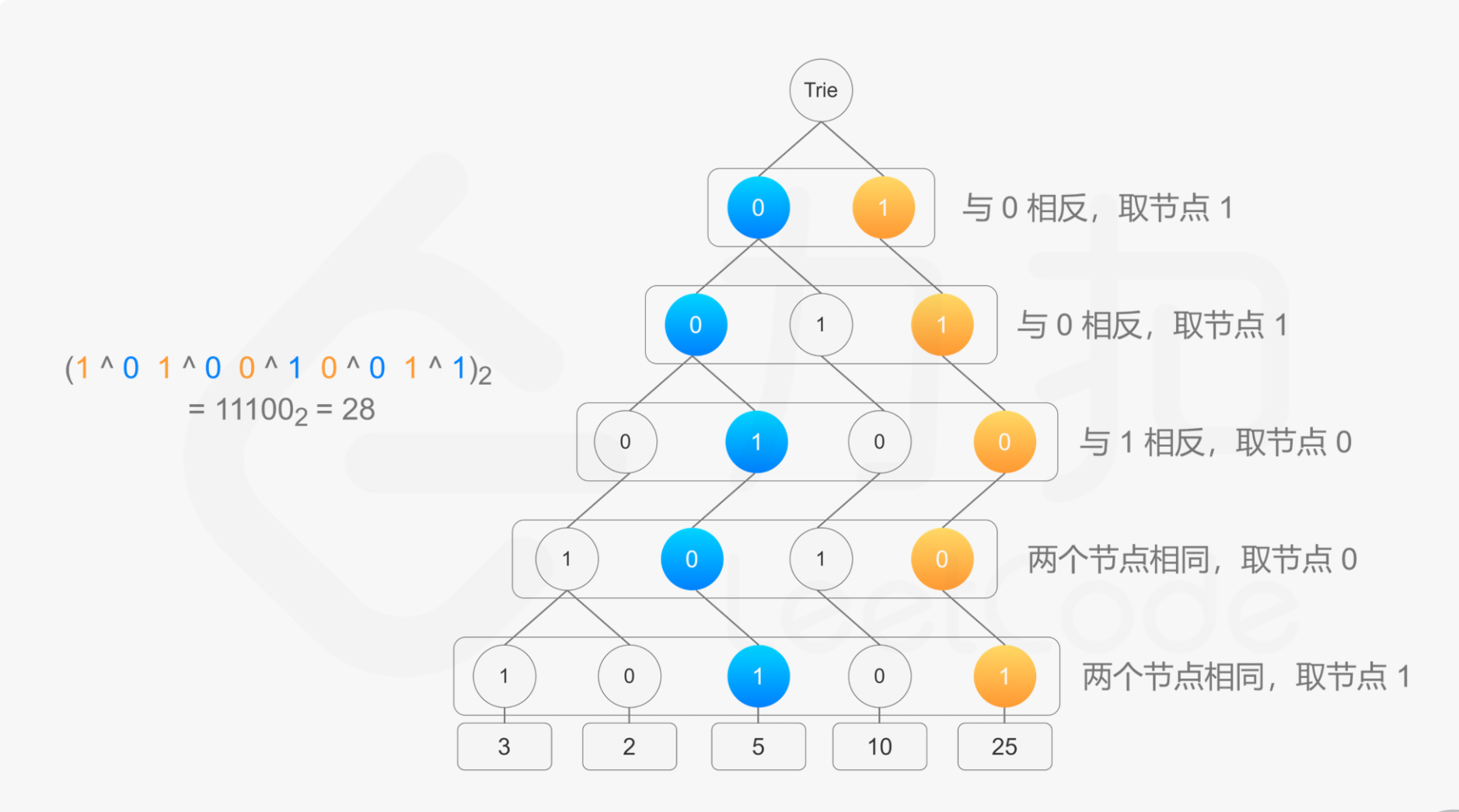
题目中给定了限制条件mi,这就需要离线查询的思想,将queries按照第二个元素从小到大进行排列,每次只向前缀树插入nums[i] <= queries[j][1]的元素,这样能够保证这个每次求取异或值的过程中前缀树中只包含符合条件的值。最后的返回结果需要按照queries的顺序重新排列。
public int[] maximizeXor(int[] nums, int[][] queries) {
int[][] que = new int[queries.length][3];
Arrays.sort(nums);
for (int i = 0; i < queries.length; i++) {
que[i][0] = queries[i][0];
que[i][1] = queries[i][1];
que[i][2] = i;
}
Arrays.sort(que, (o1, o2) -> (o1[1] - o2[1]));
Node root = new Node();
int[] ret = new int[que.length];
int pos = 0;
for (int i = 0; i < que.length; i++) {
int max = que[i][1];
while (pos < nums.length && nums[pos] <= max) {
root.insert(nums[pos]);
pos++;
}
ret[que[i][2]] = root.maxXor(que[i][0]);
}
return ret;
}
private class Node {
Node[] next;
public Node() {
next = new Node[2];
}
public void insert(int n) {
Node node = this;
for (int i = 0; i < 31; i++) {
int temp = (n >> (30 - i)) & 1;
if (temp == 0) {
if (node.next[0] == null) {
node.next[0] = new Node();
}
node = node.next[0];
} else {
if (node.next[1] == null) {
node.next[1] = new Node();
}
node = node.next[1];
}
}
}
public int maxXor(int n) {
Node node = this;
int ret = 0;
for (int i = 0; i < 31; i++) {
if (node.next[1] == null && node.next[0] == null) return -1;
int temp = (n >> (30 - i)) & 1;
if (temp == 0) {
if (node.next[1] != null) {
node = node.next[1];
ret = ret | (1 << (30 - i));
} else {
node = node.next[0];
}
} else {
if (node.next[0] != null) {
node = node.next[0];
} else {
node = node.next[1];
ret = ret | (1 << (30 - i));
}
}
}
return n ^ ret;
}
}
}