2021-04-16 2021-04-16 约 18133 字预计阅读 37 分钟

1 Introduction

CS61B Spring 2018课程网址: https://sp18.datastructur.es/

推荐的Java参考书：Head First Java

1.1 Java Intro

Java是一门静态类型编译型的语言，源文件类型为.java，经过javac编译器将其编译为.class文件，此时.class文件是已经经过类型检查的，再用java解释器去执行这个.class文件

Java是纯面向对象语言，所有的函数都在一个class中。

示例：

/* Dog.java */
public class Dog {
    public int weightInPounds;
    
    /* one integer constructor for dogs */
    public Dog(int w) {
        weightInPounds = w;
    }
    
    public void makeNoise() {
        if (weightInPounds < 10) {
            System.out.println("yip!");
        } else if (weightInPounds < 30) {
            System.out.println("bark");
        } else {
            System.out.println("wooof!");
        }
    }
}

/* DogLauncher.java */
public class DogLauncher {
    public static void main(String[] args) {
        Dog d = new Dog();
        d.weightInPounds = 51;
        d.makeNoise();
    }
}

> javac Dog.java
> javac DogLauncher.java
> java DogLauncher
wooof!

注意：这里的makeNoise方法是一个non-static方法，也就是一个实例方法。如果一个方法是被一个实例调用的，那么这个方法必须是non-static

如果想创建一个元素为对象的数组：

声明一个该类型的数组变量
对该数组的每个元素用new创建一个新的对象并赋值

Dog[] dogs = new Dog[2];
dogs[0] = new Dog(8);
dogs[1] = new Dog(20);
dogs[0].makeNoise();

enhanced for loop

如果在for循环中对Index不感兴趣，可以采用:实现循环，比如

String[] a = {"cat", "dog", "laser horse"};
for (String s : a) {
    if (s.contains("horse")) {
        continue;
    }
    System.out.println(s);
}

1.2 JUnit

JUnit是一个单元测试包，在进行单元测试时调用

import org.junit.Test;
import static org.junit.Assert.*;

@Test
public class TestSort {
    public void testSort() {
        String[] input = {"i", "have", "an", "egg"};
        String[] expected = {"an", "egg", "have", "i"};
        
        Sort.sort(input);
        assertArrayEquals(expected, input);
    }
}

注意：所有的test方法都必须是non-static

2 List

2.1 SLList (Singly Linked List)

Java中实现List的方法：

public class IntNode {
    public int item;
    public IntList next;
    
    public IntNode(int i, IntNode n) {
        item = i;
        next = n;
    }
}

public class SLList {
    public IntNode first;
    
    public SLList(int x) {
        first = new IntNode(x, null);
    }
    
    /** Adds an item to the front of the list */
    public void addFirst(int x) {
        first = new IntNode(x, first);
    }
    
    public int getFirst() {
        return first.item;
    }
    
    public static void main(String[] args) {
        SLList L = new SLList(15);
        L.addFirst(10);
        int x = L.getFirst();
        // outputs 10
    }
}

private关键字

如果将SLList类中的first修改为

private IntNode first;

则在另一个class中不能够直接访问这个first变量，但是可以通过public void addFirst等public方法去修改和访问first

Nested Class

可以在一个class中嵌套另一个class，比如

public class SLList { 
    private class IntNode {
        public int item;
        public Node next;

        public IntNode(int i, IntNode n) {
            item = i;
            next = n;
        }
    }
    public IntNode first;
    public SLList(int x) {
        first = new IntNode(x, null);
    }
    
    /** Adds an item to the front of the list */
    public void addFirst(int x) {
        first = new IntNode(x, first);
    }
    
    public int getFirst() {
        return first.item;
    }
    
    public static void main(String[] args) {
        SLList L = new SLList(15);
        L.addFirst(10);
        int x = L.getFirst();
    }
}

因为IntNode class是依附于SLList class的，因此可以将其放在SLList中

helper function

class中可以用private static来修饰helper function，表明这个函数不能被外界访问，比如想要获取一个SLList的大小

private static int size(IntNode p) {
    if (p.next == null) {
        return 1;
    }
    return 1 + size(p.next);
}

public int size() {
    return size(first);
}

2.2 DLList(Doubly-Linked List)

双向链表：一个Node除了拥有指向下一个Node的指针之外，还拥有指向前一个node的指针

sentinel node：哨兵节点，是实际上的第一个节点，但是并不包含在概念中的链表中，这是为了方便实现addLast方法而添加的。这个哨兵节点的item值可以为任意值，因为不会使用它。

在DLList中，可以有一种Circular Sentinel或者Double Sentinel的模式

在Double Sentinel中，在最开始和最结尾处都有一个Sentinel Node，SentFront的next指向第一个真正的节点，prev指向null，而SentBack的next指向Null，prev指向最后一个真正的节点

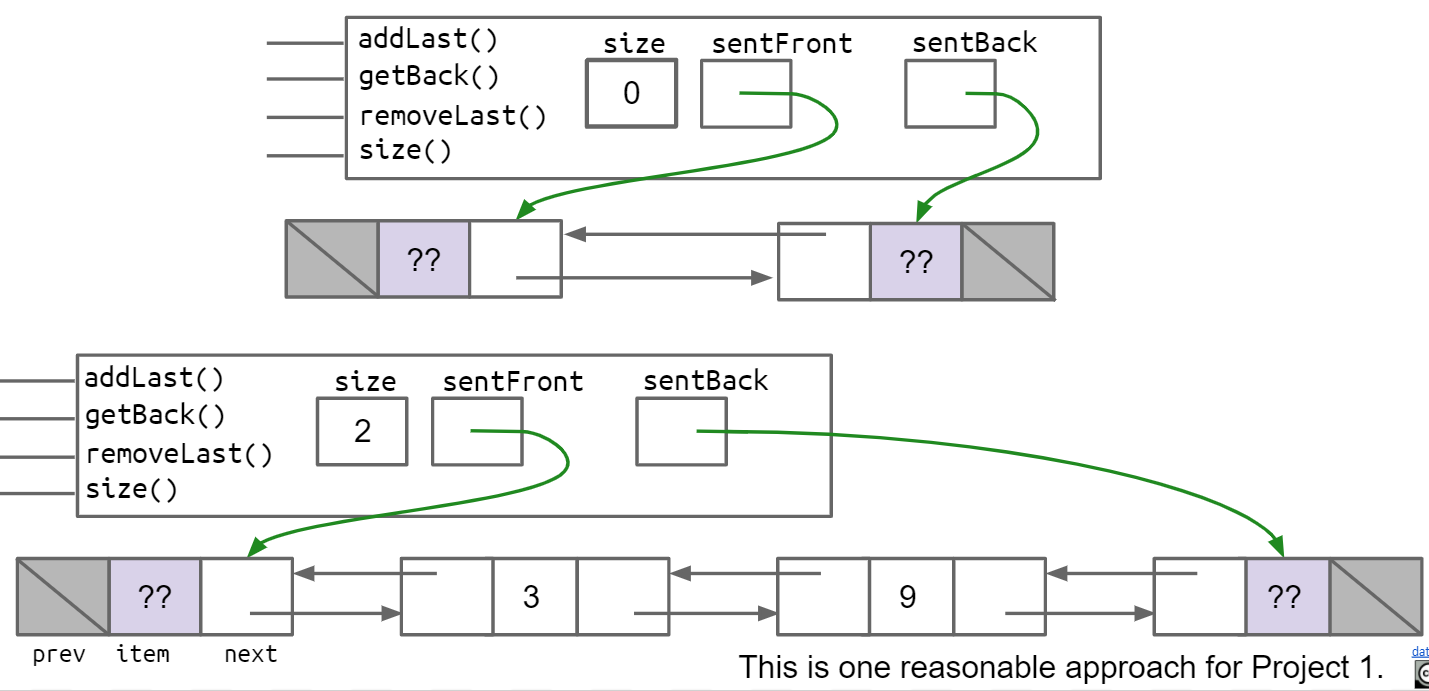
Circular Sentinel则只需要一个sentinel node，这个sentinel node的next指向第一个真正的节点，prev指向最后一个真正的节点，如果没有节点，则prev和next都指向自己

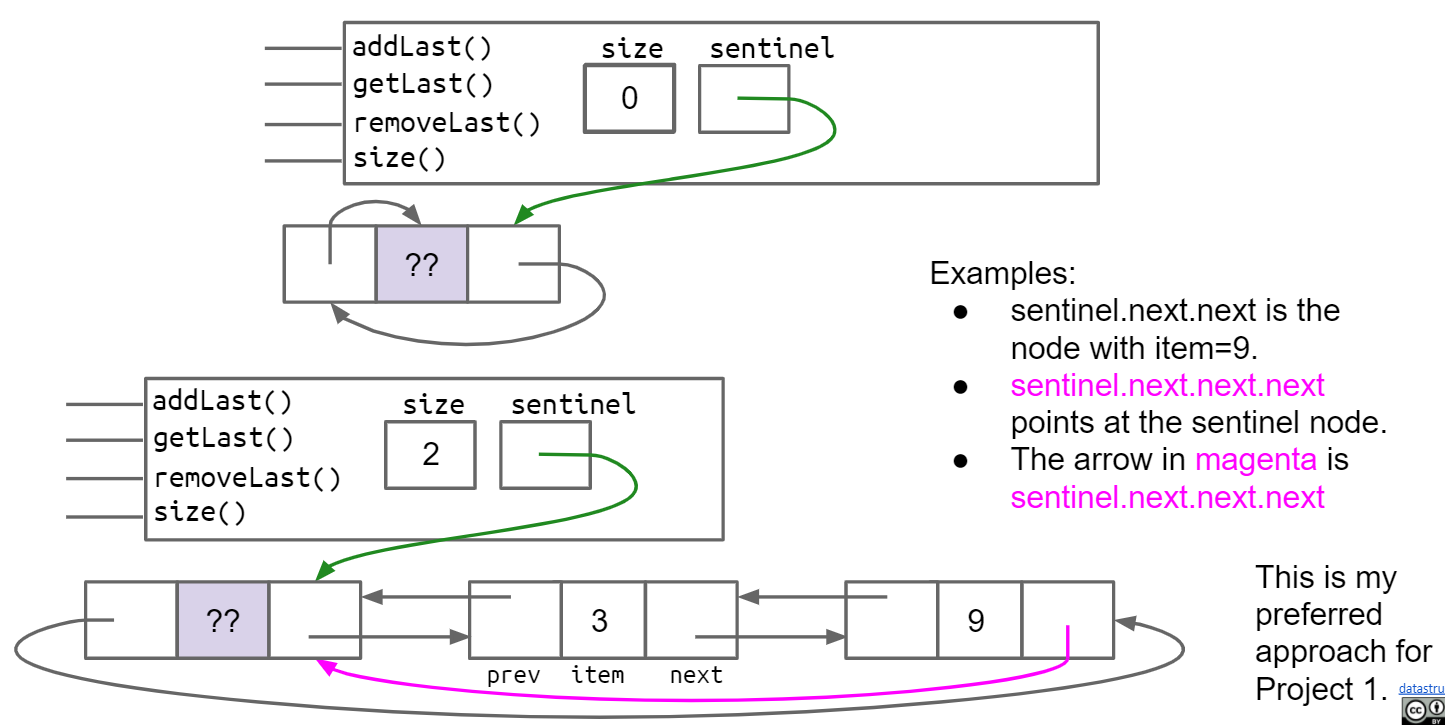
2.3 Generic List / Template

Java提供泛型(Generic)支持，这样就可以让我们的List不仅支持int，也可以支持其他比如String等类型

在class名称后添加<PLACEHOLDER>，PLACEHOLDER代表类型

public class SLList<T> { 
    private class Node {
        public T item;
        public Node next;

        public Node(T i, Node n) {
            item = i;
            next = n;
        }
    }
    public Node first;
    public SLList(T x) {
        first = new IntNode(x, null);
    }
    
    /** Adds an item to the front of the list */
    public void addFirst(T x) {
        first = new Node(x, first);
    }
    
    public T getFirst() {
        return first.item;
    }
    
    public static void main(String[] args) {
        SLList<String> L = new SLList<>(15);
        // or SLList<String> L = new SLList<String>(15);
        L.addFirst("thugs");
        String x = L.getFirst();
    }
}

在泛型中primitive type需要声明为reference type(Java封装类)，比如

int -> Integer
double ->Double
char -> Character
boolean -> Boolean
long -> Long

2.4 AList (Array List)

Array是一种特殊类型的对象，包含了一连串内存空间，可以通过A[i]来获取A中第i个item。而一个类的实例是需要用一个名称，比如A.item来获取数据的。

Array有一个固定的长度

三种声明array的方法：

y = new int[3];
x = new int[]{1, 2, 3, 4, 5};
int[] w = {9, 10, 11, 12, 13};

2D Array

2D Array的声明

int[][] pascalsTriangle;

实例化一个包含了4个1D Array的2D Array并赋值给变量

pasacalsTriangle = new int[4][];

实例化一个包含了一个int的1D Array并赋值给变量

pascalsTriangle[0] = new int[]{1};

也可以直接声明一个包含了4个[包含5个int的1D Array]的2D Array并赋值给变量

int[][] matrix;
matrix = new int[4][4];

或者声明、实例化、赋值放在一起

int[][] pascalAgain = new int[][]{ {1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}};

AList

public class AList<T> {
    private T[] items;
    private int size;
    
    /** creates an empty list */
    public AList() {
        items = (T[]) new Object[100];  // 注意：这里用了casting，这是因为Java中不能有泛型对象array，所以先new一个Object array然后进行类型转换
        size = 0;
    }
    
    public void resize(int capacity) {
        T[] a = (T[]) new Object[capacity];
        System.arraycopy(items, 0, a, 0, size);
        items = a;
    }
    
    /** Inserts X into the back of the list */
    public void addLast(T x) {
        // resize items since its full
        if (size == items.length) {
			resize(size * 2); 
        }
        items[size] = x;
        size = size + 1;
    }
    
    public T getLast() {
        return items[size - 1];
    }
    
    public int removeLast() {
        int last = getLast();
        items[size-1] = null;  // 这一步可以不写，但是为了防止loitering，即保留对不需要的对象的引用（会导致gc无法将其回收），最好将删除的item给null out
        size = size - 1;
        return last;
    }
}

当item的空间大小不足时，可以用resize(size * 2)来扩展空间，每次扩展2倍大小的空间可以防止addLast频繁调用resize造成程序运行时间的指数级增长。

3 Inheritance

3.1 Intro and Interfaces

Java中一个类中可以有多个同名方法，但是函数签名可以不同

public static String longest(SLList<String> list)

public static String longest(AList<String> list)

这叫做method overloading，当调用了WordUtils.longest时，Java会根据传入的参数的种类自动调用正确的方法

但是我们不想为每个相似的类都重写一个方法

Java中有一种特殊的抽象类叫做接口（interface），这种抽象类中只包含常量和方法的定义，而没有变量和方法的实现

public interface List61B<T> {
    public voif addLast(T x);
    public T getLast();
    public T get(int i);
    public int size();
    public T removeLast();
    public void insert(T x, int position);
    public void addFirst(T x);
    public T getFirst();
}

然后我们使用implements这个关键字来告诉Java编译器SLList和AList是List61B的下位

public class AList<T> implements List61B<T> {
    ...
    public void addLast(T x) {
        ...
    }
}

这样我们就可以重新实现public static String longest(List61B<String> list)来实现这样一个上位方法。

3.2 Overriding & Overloading

如果一个子类有一个和父类的签名完全一样的方法，那么我们说这个子类重写(override)了这个方法

如果子类的方法名和父类方法名相同或者同一个类中有相同的方法名，但是签名不同，那么我们说这个子类overload了这个方法

最好对每个被重写的方法都加上@Override的annotation，即使不加也能编译通过，但是加上可以在编译时检查重写时函数签名有没有写错。

3.3 Inheritance

interface inheritance

使用implements来实现interface，就是一种Interface inheritance

子类必须实现所有interface中的方法，否则无法编译通过

Implementation inheritance

interface中其实还可以有函数实现，但是必须要在函数签名前面加上default关键字

public interface List61B<T> {
    ...
    default public void print() {
        for (int i = 0; i < size(); i += 1) {
            System.out.print(get(i) + " ");
        }
        System.out.println();
    }
}

这样即使在被继承的类（比如SLList）中没有声明print方法也没有问题。该特性从Java8才开始支持。

由于SLList中的get是从头或尾开始一个一个查找的，因此List61B中的default print方法效率很低，可以选择在SLList这个类中重写print方法（尽管并不是必须重写的），这样对SLList类型的instance调用print方法将调用该方法

@Override
public void print() {
    for (Node p = sentinel.next; p != null; p = p.next) {
        System.out.print(p.item + " ");
    }
}

extends

如果想从一个class而不是interface继承，使用extends关键字

e.g. 从SLList继承一个RotatingSLList类

public class RotatingSLList<Item> extends SLList<Item> {
    /** Rotates list to the right */
    public void rotateRight() {
        Item x = removeLast();
        addFirst(x);
    }
}

extends可以让RotatingSLList继承SLList所有的实例和静态变量，继承所有的方法和嵌套的类，但是构造器不能继承，private修饰的也不能继承

当子类的重写方法需要引用父类的方法时，可以使用super关键字来指代父类

子类的构造器中如果没有显式地声明父类构造器，那么Java将会自动调用super()来调用一个父类构造器，但是调用的可能不是你想要的父类构造器，因此最好显式声明想要调用的父类构造器

3.4 Static Type v.s. Dynamic Type

Java中所有的变量都有一个静态种类（编译时种类，在变量声明时决定）和一个动态种类（运行时种类，在变量实例化和赋值时决定）

public static void main(String[] args) {
    LivingThing lt1;
    lt1 = new Fox();
    Animal a1 = lt1;
}

变量	静态种类	动态种类
lt1	LivingThing	Fox
a1	Animal	Fox

当我们调用了一个变量的方法，这个变量的静态种类为A而动态种类为B时，如果B重写（而不是overload，必须要保证函数签名一致)了这个方法，那么会调用B类的方法，这叫做动态方法选择

但是在编译时，会根据静态种类进行编译，比如动态种类Fox有一个方法foxsound()，静态种类LivingThing并没有这个方法，那么lt1.foxsound()将造成编译错误

再比如：如果Poodle是Dog的子类，Dog有一个方法public static Dog maxDog(Dog d1, Dog d2) {...}

Poodle frank = new Poodle("Frank", 5);
Poodle frankjr = new Poodle("Frank Jr.", 15);

Dog largerDog = maxDog(frank, frankjr);  // compiles, bc Right Hand Side (RHS) expression is type Dog, and LHS expression is Dog, so can be assigned
Poodle largerPoodle = maxDog(frank, frankjr);  // cannot compile, bc RHS expression is static type Dog, and LHS type is Poodle, and Dog "is not" Poodle (but Poodle "is" Dog)

但是可以使用casting强制类型转换来转换任意表达式的静态类型，比如

Poodle largerPoodle = (Poodle) maxDog(frank, frankjr);  // compiles

3.5 Higher Order Functions

Java7及以前的高阶函数

变量的memory box中不能有指向函数的指针

采用Interface Implementation的方式去解决

/** reprensent a function that takes in an integer and returns an integer */
public interface IntUnaryFunction {
    int apply(int x);
}

public class TenX implements IntUnaryFunction {
    public int apply(int x) {
        return 10 * x;
    }
}

/** Demonstrates higher orfer functions in java */
public class HofDemo {
    public static int do_twice(IntUnaryFunction f, int x) {
        return f.apply(f.apply(x));
    }
    
    public static void main(String[] args) {
        IntUnaryFunction tenX = new TenX();
        System.out.println(do_twice(tenX, 2))
    }
}

3.6 Polymorphism

多态：一个interface可以被多种子类继承，注意和多继承不一样，多继承是一个子类继承多个父类，而不是一个父类被多个子类继承。Java允许一个子类implements多个接口

比如要实现一个比较函数，使得该函数可以应用于任意class上。先定义一个interface，里面需要有一个比较方法，然后让子类去实现这个interface

public interface OurComparable {
    /** returns -1 if this < o
     *  0 if this equals o
     *  1 if this > o */
    public int compareTo(Object o);
}

public class Dog implements OurComparable {
    private String name;
    private int size;
    
    public Dog(String n, int s) {
        name = n;
        size = s;
    }
    
    public void bark() {
        System.out.println(name + " says: bark");
    }
    
    public int compareTo(Object o) {
        Dog uddaDog = (Dog) o;
        if (this.size < udda.size) {
            return -1;
        } else if (this.size == uddaDog.size) {
            return 0;
        } else {
            return 1;
        }
    }
}

但是OurComparable的问题在于其他的class并没有实现这个接口，因此要让其他class也能进行比较，需要对他们全部进行重写，这是很麻烦的。解决方案是：让Max基于Java内建的Comparable<T>接口来实现

public interface Comparable<T> {
    public int compareTo(T obj);  
}

public class Dog implements Comparable<Dog> {
    // 因为使用了泛型，就不再需要使用强制类型转换
    public int compareTo(Dog uddaDog) {
        return this.size - uddaDog.size;
    }
}

comparator

在java.util.Comparator中，比较器可以用来指定这个类如何实现比较，从而可以不用继承Comparable接口

import java.util.Comparator;
public class Dog {
    ...;
    public class NameComparator implements Comparator<Dog> {
        public static int compare(Dog a, Dog b) {
            return a.name.compareTo(b.name);
        }
    }
}

public class DogLauncher {
    public static void main(String[] args) {
        Dog d1 = new Dog("Elyse", 3);
        Dog d2 = new Dog("Benjamin", 15);
        
        Dog.NameComparator nc = new Dog.NameComparator();
        if (nc.compare(d1, d3) > 0) {
            d1.bark();
        } else {
            d3.bark();  // compare alphabetically
        }
    }
}
// Elyse says: bark

回调函数：作为参数被传入的一个函数。在Python中，函数可以直接作为参数被传入，Java中，这个回调函数被打包在一个接口中。

3.7 Abstract class

抽象类用abstract修饰，抽象类的子类继承了父类的全部特性，子类用extends继承抽象类。抽象类本身不能被实例化，因此所有抽象类必须被继承才能使用。

抽象类中默认的是普通方法，可以加上abstract声明抽象方法。抽象方法是指当父类的某些方法还不确定的时候在后面让子类进行重用。
同时抽象类中可以有普通变量，而接口中只能存在被public static final修饰的静态最终常量。
抽象类中的方法修饰符可以是public、private和protected，而接口中的方法一定是public
Java中只能存在单继承，即所有抽象类只能单继承，但是接口可以做到多实现，即一个类可以implements多个接口

public abstract class GraphicObject {
    public int x, y;
    public void moveTo(int newX, int newY) {...}
    public abstract void draw();
}

所有实现某个接口的类必须实现这个接口中声明的所有方法，否则必须声明为抽象类。同时抽象类中也可以声明除了从接口中继承来的其他方法

3.8 Prebuilt ADT

Java.util库中有几种prebuilt ADT，包括：

List：有序集合，子类包括LinkedList、ArrayList
Set：无序集合，子类包括HashSet、TreeSet
Map：键值对集合，与Python中的字典一样，子类包括HashMap、TreeMap

4 Java Syntax

4.1 Reference

Java中有8个primitive types，包括int、double、float、char等，这些类型的值是直接存储在变量中的，但是object是一种引用类型，变量存储的是这个object的地址（指针）而不是它的数据。

array也是一种对象，比如

int[] a = new int[]{0, 1, 2, 95, 4};

第一步是int[] a，这是变量声明（declaration），在栈中创建了一个变量并分配给它64位大小的空间用来存储地址。然后用new在堆中分配了一个int[]对象，里面存储了0、1、2、95、4等数据，这叫做对象的实例化（instantiation）。最后将这个对象的地址放到变量中，这叫做分配（assignment）

4.2 Static

1） static方法是类方法，不需要依附于对象即可使用，不能访问实例成员变量，也不能使用非静态成员方法，通过<classname>.method调用。non-static方法是实例方法，通过<objectname>.method调用。

有些类是永远不会被实例化的，因此只能使用static方法，比如

x = Math.round(5.6);

2）用static修饰的变量名是静态变量，也叫做类变量，这个变量是被该类中的所有实例共享的，既可以用<classname>.varaiblename访问，也可以用<objectname>.varaiblename访问

this：相当于python中的self

3） static代码块：只会在类加载的时候执行一次，以优化程序性能

class Person {
    private Date birthDate;
     
    public Person(Date birthDate) {
        this.birthDate = birthDate;
    }
     
    boolean isBornBoomer() {
        Date startDate = Date.valueOf("1946");
        Date endDate = Date.valueOf("1964");
        return birthDate.compareTo(startDate)>=0 && birthDate.compareTo(endDate) < 0;
    }
}

上述例子中，每次调用isBornBoomer()都会创建startDate和endDate，而采用static代码块后，只会创建一次

class Person {
    private Date birthDate;
    private static Date startDate,endDate;
    static{
        startDate = Date.valueOf("1946");
        endDate = Date.valueOf("1964");
    }
     
    public Person(Date birthDate) {
        this.birthDate = birthDate;
    }
     
    boolean isBornBoomer() {
        return birthDate.compareTo(startDate)>=0 && birthDate.compareTo(endDate) < 0;
    }
}

因此static代码块中可以执行只需要进行依次的初始化操作

判断以下代码的输出结果

ublic class Test extends Base {
 
    static{
        System.out.println("test static");
    }
     
    public Test(){
        System.out.println("test constructor");
    }
     
    public static void main(String[] args) {
        new Test();
    }
}
 
class Base {
     
    static{
        System.out.println("base static");
    }
     
    public Base(){
        System.out.println("base constructor");
    }
}

base static
test static
base constructor
test constructor

在执行开始先寻找main()方法，因为这是程序的入口。在执行main()方法之前必须先加载Test类，而在加载Test类的时候发现该类继承自Base类，因此先去加载Base类，然后发现有static块，便执行该块，Base类加载完成之后继续加载Test类，然后发现Test类中也有static块，便执行static块，在加载完所需的类之后，便开始执行main()方法。在main()方法中执行new Test()的时候会先调用父类的构造器，然后再调用自身的构造器。因此，便出现了上面的输出结果

4.3 Autoboxing & Auto-unboxing

可以在包装类和原始类之间进行隐式转化

public class BasicArrayList {
    public static void main(String[] args) {
        ArrayList<Integer> L = new ArrayList<Integer>();
        L.add(5);   // 正常情况下应该是L.add(new Integer(5))
        int first = L.get(0);  // 正常情况下应该是L.get(0).valueOf();
    }
}

4.4 Immutability

加上final关键字使一个变量变为不可变的变量，即在实例化之后不能再进行赋值

String也是一个不可变的对象

注意：将一个reference声明为final并不能让这个对象不可变，比如

public final ArrayDeque<String> d = new ArrayDeque<String>();

4.5 Generic Method

当只希望让类中的方法变为generic，而不是整个类变成generic时，可以直接在方法名前面加上<>

public static <K, V> K get(Map61B<K, V> sim, K key);

在generic method中使用compareTo，因为编译器不知道这个generic type是否能够进行比较，因此会报错，为了解决这个问题，需要显式地声明generic type extends Comparable，这叫做type upper bound，表示这个generic type是Comparable的子类

public static <K extends Comparable<K>, V> K maxKey(Map61B<K, V> map) {
    List<K> keylist = map.keys();
    K largest = keylist.get(0);
    for (K k : keylist) {
        if (k.compareTo(largest) > 0) {
            largest = k;
        }
    }
    return largest;
}

4.6 Exception

可以显式地throw一个exception

public V get(K key) {
    int index = keyIndex(key);
    if (index == -1) {
        throw new IllegalArgumentException("The key provided " + key + " was not in ArrayMap");
    }
}

Java本身也可以隐式地抛出一个异常

被抛出的异常可以被catch，从而避免程序崩溃

try {
    d.receivePat();
} catch (Exception e) {
    System.out.println("Tried to pat: " + e);
}

checked exceptions：

编译器要求这些异常必须被catch，从而避免那些能够被避免的程序崩溃

e.g.

public class Eagle {
    public static void gulgate() {
        if (today == "Thursday") {
            throw new IOException("hi");
        }
    }
}

提示：

ERROR: unreported exception IOException; must be caught or declared to be thrown

所有的RuntimeException的子类或者Error的子类都是unchecked，其他所有的Throwable都是checked

对于checked异常，除了用catch来确保这些异常都被接住之外，也可以用throws关键字来修饰这个方法，从而让其他程序来处理这个异常

public static void gulgate() throws IOException {
    ...throw new IOException("hi");...
}

当另一个方法使用了这个可能抛出checked异常的危险方法之后，这个方法本身也变得危险，因此需要catch或者本身写为throws

4.7 Iterators

Java中有enhanced for loop，类似于Python的for ... in

List<Integer> friends = new ArrayList<Integer>();
friends.add(5);
friends.add(23);
friends.add(42);
for (int x : friends) {
    System.out.println(x);
}

Iterator使用方法：

Iterator<Integer> seer = friends.iterator();
while (seer.hasNext()) {
    System.out.println(seer.next());
}

如果要正常使用上述iterator，必须要保证List<T>有iterator()方法可以让List继承iterable接口，从而继承iterator()这个抽象方法

public interface List<T> extends Iterable<T> {
    ...
}

public interface Iterable<T> {
    Iterator<T> iterator();
}

package java.util;
public interface Iterator<T> {
    boolean hasNext();
    T next();
}

e.g.

比如想让我们自定义的ArrayMap能够使用enhanced for loop，需要提供一个KeyIterator class(nested in ArrayMap class)从而实现hasNext()、next()等方法

public class KeyIterator implements Iterator<K>{
    private int ptr;
    public KeyIterator() {
        ptr = 0;
    }
    public boolean hasNext() {
       return (ptr != size);
    }
    public K next() {
        K returnItem = keys[ptr];
        ptr = ptr + 1;
        return returnItem;
   }
}

如果要实例化一个KeyIterator对象(nested class)，需要dot notation后面再接一个new

ArrayMap<String, Integer> am = new ArrayMap<String, Integer>();
am.put("hello", 5);
am.put("syrups", 10);
ArrayMap.KeyIterator ami = am.new KeyIterator();
while (ami.hasNext()) {
   System.out.println(ami.next());
}

但是尽管我们当前有一个自定义的KeyIterator类，但是我们需要一个iterator()方法（因为我们要继承Iterable接口）

public Iterator<K> iterator() {
    return new KeyIterator();
}

最后要让ArrayMap也继承Iterable接口

public class ArrayMap<K, V> implements Map61B<K, V>, Iterable<K> {
    ...
}

4.8 Access Control

Modifier	Class	Package	Subclass	World
public	Y	Y	Y	Y
protected	Y	Y	Y	N
	Y	Y	N	N
private	Y	N	N	N

当没有任何access modifier时，相同包的其他class(但不包括子类)可以访问，这也叫做’package private'

side note: 为什么没有modifier的时候package中的变量可以被访问而subclass中的不能被访问？

因为很多情况下人们会继承一个自己并不熟悉的class，因此如果subclass中的变量能够被访问就很危险，但是同一个Package往往是很多熟悉的人一起工作编写的，因此最好能够访问同一个package中的变量

类只能用public或package private（即没有修饰符）修饰。

注意：编译器对访问权限的判断只基于静态类型

e.g.

package universe;
public interface Blackhole {
    void add(Object x);
}

package universe;
public class CreationUtils {
    public static BlackHole hirsute() {
        return new HasHair();
    }
}

package universe;
class HasHair implements BlackHole {
    Object[] items;
    public void add(Object o) {...}
    public Object get(int k) {...}
}

判断下面的代码能否编译

import static CreationUtils.hirsute;
class Client {
    void demoAccess() {
        BlackHole b = hirsute();  // Sentence 1
        b.add("horse");  // Sentence 2
        b.get(0);  // Sentence 3
        HasHair hb = (HasHair) b;  // Sentence 4
    }
}

首先，HasHair这个class前面没有任何access modifier，因此是package private的，而目标代码并不处于universe包中，因此理论上目标代码无法访问HasHair这个类。但是Sentence 1中b的静态类型是BlackHole，而BlackHole这个类是public的，因此Sentence 1可以被编译（是否能被编译基于的是静态类型）。我们可以发现，尽管我们不能直接拥有一个对HasHair类型的引用，但是我们仍然可以通过一个能够引用该类并将其返回的方法获得一个动态类型为HasHair的引用。

而BlackHole这个接口中有add()方法。注意：由于Java接口中的方法默认用public abstract修饰，变量用public static final修饰，因此void add()这个方法看起来没有修饰符，但其实并不是package private而是public，因此Sentence 2是可以访问add方法的

对于Sentence 3来说，由于get()方法是在HasHair这个类中的，而这个类是package private，对Client是不可见的，因此这句话会导致编译错误

Sentence 4这句话中由于HasHair对Client不可见，因此编译错误

5 Java Miscellaneous

5.1 Packages

package: 包用于组织类和接口的namespace，一般的命名规则是网站名的倒序，比如com.microsoft.xxx

不同包中的类的名称可以相同，如果同时调用两个不同包中的相同类名的类时应该加上包名加以区别，从而避免名字冲突。同时限定了访问权限。

package ug.joshh.animal;  // 创建包

上述声明表明当前的class是在ug/joshh/animal这个目录下的

如果一个class没有package声明，那么它被放在了default package中，而default package是无法被导入的，因此绝大多数情况下都需要对class进行包声明（除非是很小的程序）

5.2 JAR

.jar文件实际上是将一堆.class文件进行打包后的结果

build systems

为了避免导入很多Java库，可以用build system来构建项目

Ant
Maven
Gradle

5.3 Object Methods

Object类的方法

String toString()：将一个Object转换为String的形式
boolean equals(Object obj)：判断两个Object的值是否相同，而==判断两个Object是否是同一个Object。注意：默认的equals实现是==，因此需要自己重写一个equals
Class<?> getClass
int hashCode()

6 Tree

6.1 Asymoptotic

算法复杂度分析

public static void printParty(int n) {
    for (int i = 1; i <= n; i = i * 2) {
        for (int j = 0; j < i; j += 1) {
            System.out.println("hello");
        }
    }
}

$1 + 2 + 4 + … + N \in \Theta(N)$

因为上述式子是大于N小于2N的

Merge sort复杂度Θ(NlogN)

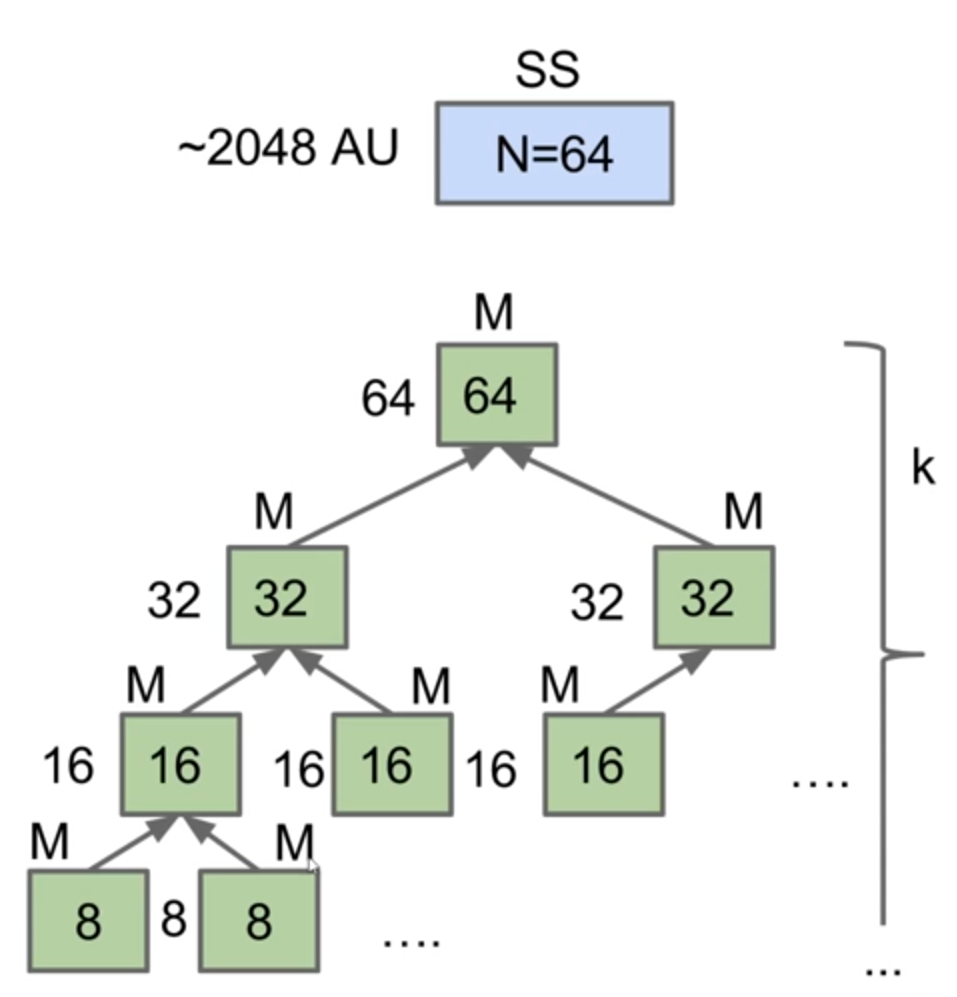
将两个sorted list合并为一个sorted list所需要的复杂度为Θ(N)，因此可以进行$log_2N$次merge实现merge sort

big Θ notation: 复杂度等于
big O notation: 复杂度小于等于
big Ω notation: 复杂度大于等于

6.2 Disjoint Sets

Disjoint Sets ADT: 并查集用来判断两个元素是否相连

connect(p, q): 将p和q相连
isConnected(p, q): 判断p和q是否相连

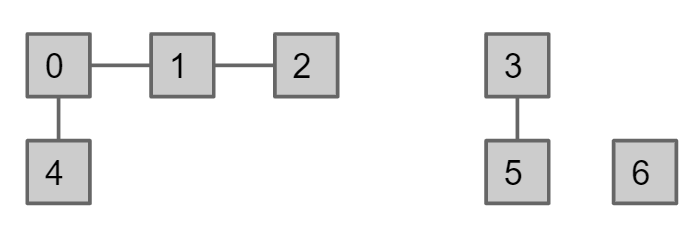
可以采用树状结构来存储数据，即数据结构中有一个parent数组，数组的index是element（p/q)，而数组的值是这个element的父节点，判断p和q是否connected只要判断这两个数的最终父节点是否相同即可

public class QuickUnionDS implements DisjointSets {
	private int[] parent;
	public QuickUnionDS(int N) {
    	    parent = new int[N];
    	    for (int i = 0; i < N; i++)
        	    parent[i] = i;
   	    }
 
  	private int find(int p) {
    	    while (p != parent[p])
        	    p = parent[p];
       	return p;
    }
    
    public boolean isConnected(int p, int q) {
		return find(p) == find(q);
}
 
    public void connect(int p, int q) {
        int i = find(p);
        int j = find(q);
        parent[i] = j;
    }
}

但是在最坏情况下，find的复杂度为O(N)（当树的branch只有一条时）

weighted quick union

记录每个tree的size（即一个tree中的元素个数，而不是树的高度），每次合并将更小size的树的根节点连接到更大size的树的根节点，这样就能避免最坏情况的形成只有一个branch的情况(实际上最高的树的高度为logN)

e.g.

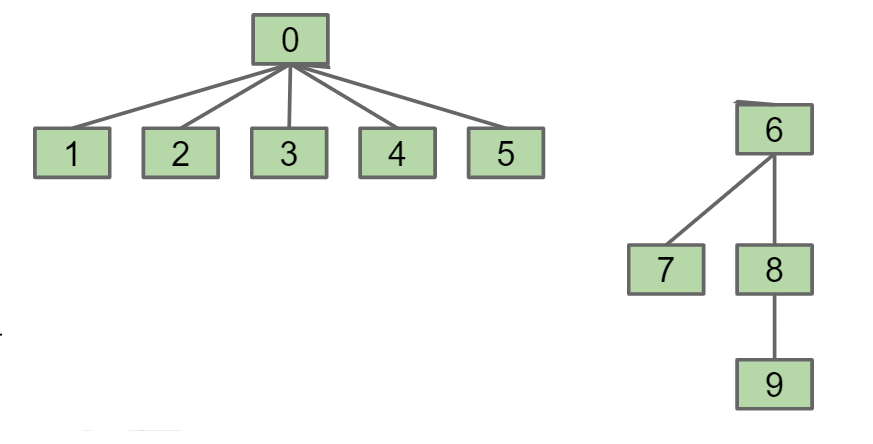
这两棵树合并时，因为前一棵树有6个元素，后一棵树只有4个元素，因此将6的父节点变为0

![image-20210402101750488]/img/posts/CS61B/image-20210402101750488.png)

public void connect(int p, int q) {
	int i = find(p);
	int j = find(q);
	if (i == j) return;
	if (size[i] < size[j]) { parent[i] = j; size[j] += size[i]; }
	else { parent[j] = i; size[i] += size[j]; }
}

weighted quick union的connect和isconnected复杂度都为O(logN)

6.3 Binary Search Tree (BST)

对于一个linked list，get()操作的最差复杂度为Θ(N)

但是可以将pointer放到中间，这样就可以将搜索时间减半，然后再将剩下一层的pointer也放到中间，再将搜索时间减半

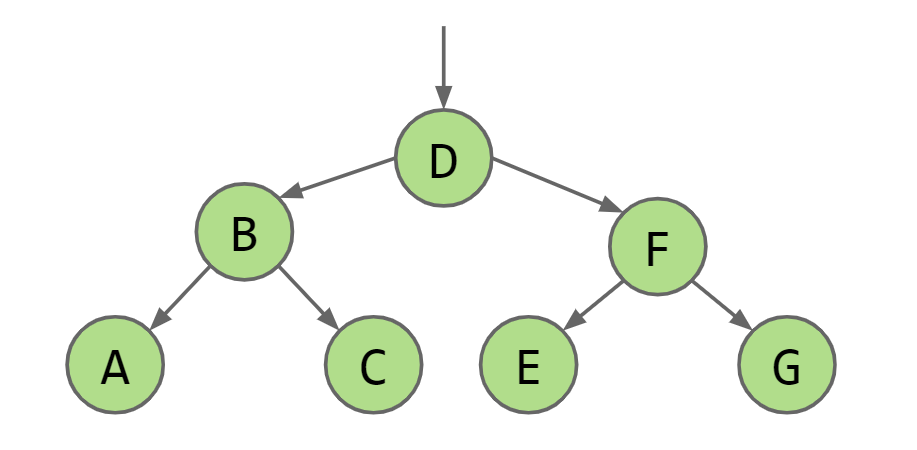
这就形成了一个二叉查找树（BST），BST中每个节点的左边的子树中的所有元素都要小于节点本身，每个节点的右边的子树中的所有元素都要大于节点本身

BST中不允许有重复的节点

BST中的节点删除

当删除的节点只有没有子节点时，直接删除，当删除的节点有一个子节点时，让这个被删除的节点的父节点指向被删除节点的子节点。当删除的节点有两个子节点时，选取这个被删除节点左侧树中最大的节点或者右侧树中最小的节点继承被删除的节点，比如上述BST中删除D，则可以将C替代D或者E替代D

/** Removes KEY from the tree if present
     *  returns VALUE removed,
     *  null on failed removal.
     */
    @Override
    public V remove(K key) {
        V ret = get(key);
        if (ret == null) {
            return null;
        }
        root = remove(key, root);
        size -= 1;
        return ret;
    }

    private Node remove(K key, Node n) {
        if (n == null) {
            return null;
        }
        int cmp = key.compareTo(n.key);
        if (cmp < 0) {
            n.left = remove(key, n.left);
        } else if (cmp > 0) {
            n.right = remove(key, n.right);
        } else {
            if (n.right == null) {
                return n.left;
            }
            if (n.left == null) {
                return n.right;
            }
            Node t = n;
            n = max(n.left);
            n.left = deleteMax(t.left);
            n.right = t.right;
        }
        return n;
    }

    private Node max(Node n) {
        if (n.right == null) {
            return n;
        }
        return max(n.right);
    }

    private Node deleteMax(Node n) {
        if (n == null) {
            return null;
        }
        if (n.right != null) {
            n.right = deleteMax(n.right);
        } else {
            return n.left;
        }
        return n;
    }

6.4 Balanced BST

如果使用传统的BST，当Insertion是按照从小到大进行的话，就会使一个树变成一个链表

Tree Rotation

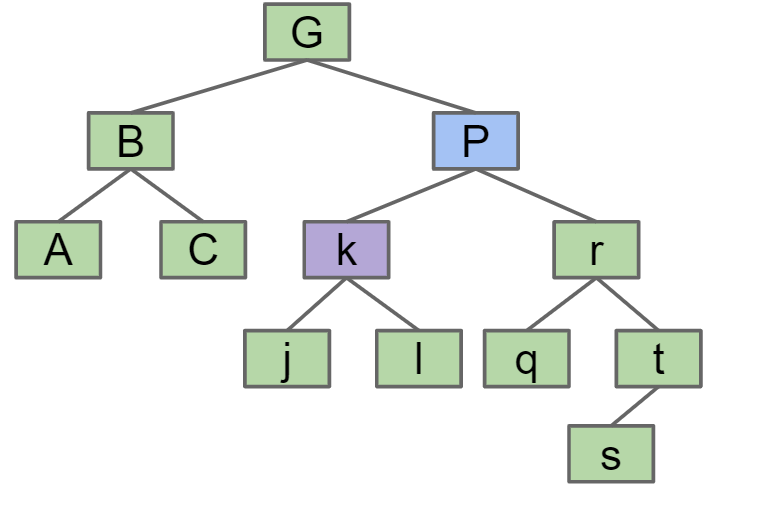
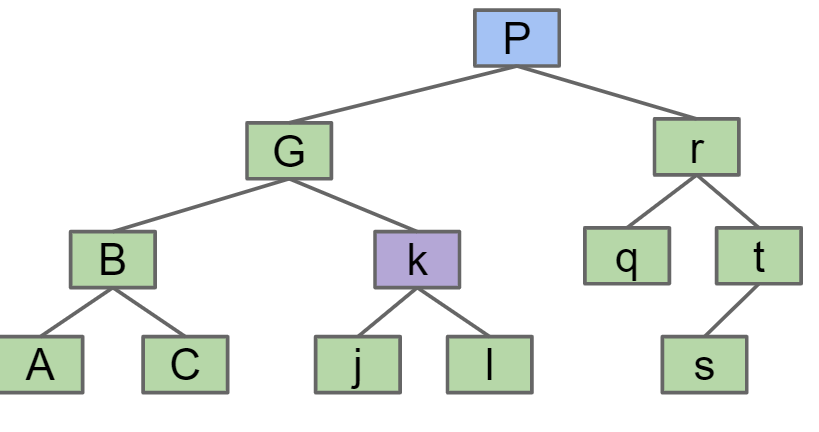
RotateLeft(G): 将G变为P的左节点，P原先的左节点变为G的右节点，假如G有父节点，则P指向G的父节点

B-Tree / 2-3 Tree

一个节点中可以有超过1个的key，比如2-3树可以一个节点有2个key，而一个节点可以有超过2个的子节点，比如2-3树中可以有3个子节点

在进行节点插入时，先根据Key的值插入到相应的叶节点上。比如向下面的2-3-4树中插入y和z，因为y和z大于m，大于oqs，因此插入到t和u这个节点上。

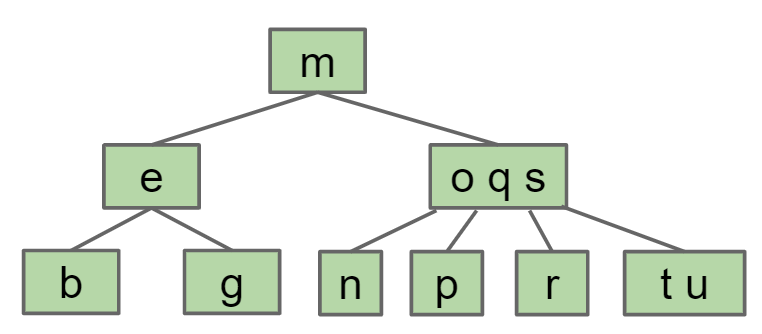
但是2-3-4树一个节点最多3个key，因此将tuyz这个节点的中间那个key也就是u移到父节点，而t小于u，因此需要将t分出来变为一个新的节点

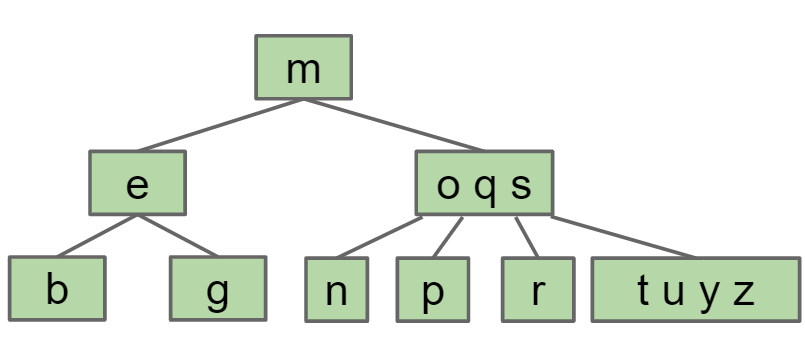
oqsu中的q移到父节点形成mq节点，而o小于q因此独立出来称为一个新的节点

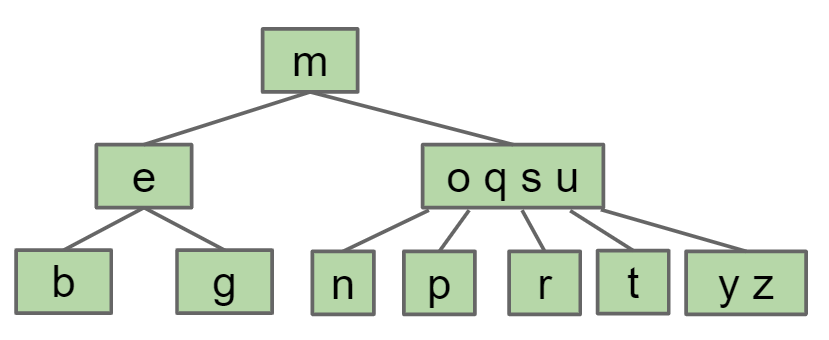
最终形成一个平衡树 B树是自平衡的

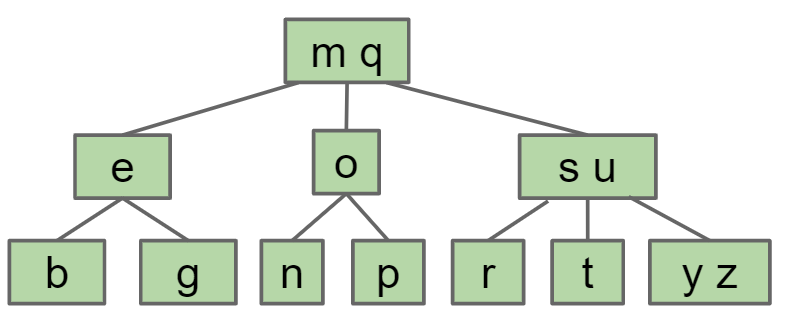
红黑树

红黑树是2-3B树的变体，为了能像2-3B树一样达到自平衡的效果而又保证每个节点只有一个Key，需要用到"glue link"，glue link两边的节点结合起来就成为了2-3B树中一个拥有2个key的节点

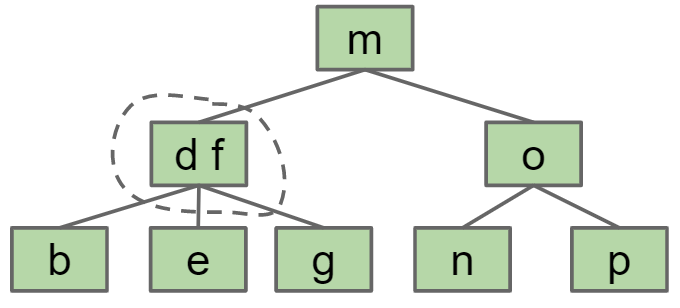
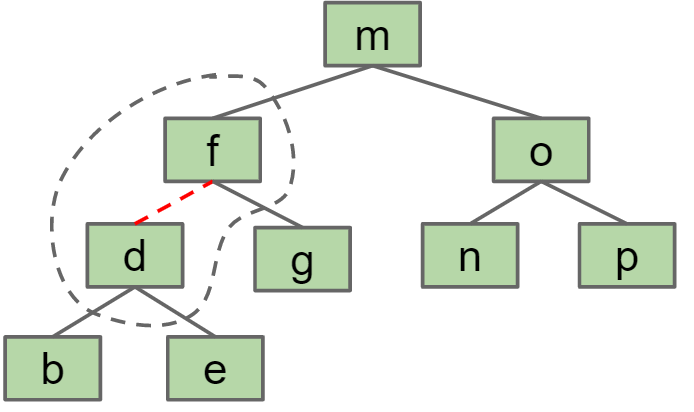
所有的红黑树都有以下性质：

没有一个节点有2个红色link，否则就称为2-3-4B树
从根节点到所有的叶节点都拥有同样数量的黑色link（假设红色link不算，那么所有黑色link形成了跟2-3-4B树相同的结构，这是一个严格平衡的树）
红黑树的最大深度小于等于其对应的2-3B树的2倍，因为每个2-3B树的节点最多只有2个key

6.5 Advanced Trees

tree traversal

breadth-first-traversal：先将一个层级的node全部遍历一遍
```
public void levelOrder(Tree T, Action toDo) {
    for (int i = 0; i < T.height(); i += 1) {
        visitLevel(T, i, toDo);
    }
}

public void visitLevel(Tree T, int level, Action toDo) {
    if (T == null) { return; }
    if (lev == 0) {
        toDo.visit(T.key);
    }
    else {
        visitLevel(T.left(), lev - 1, toDo);
        visitLevel(T.right(), lev - 1, toDo);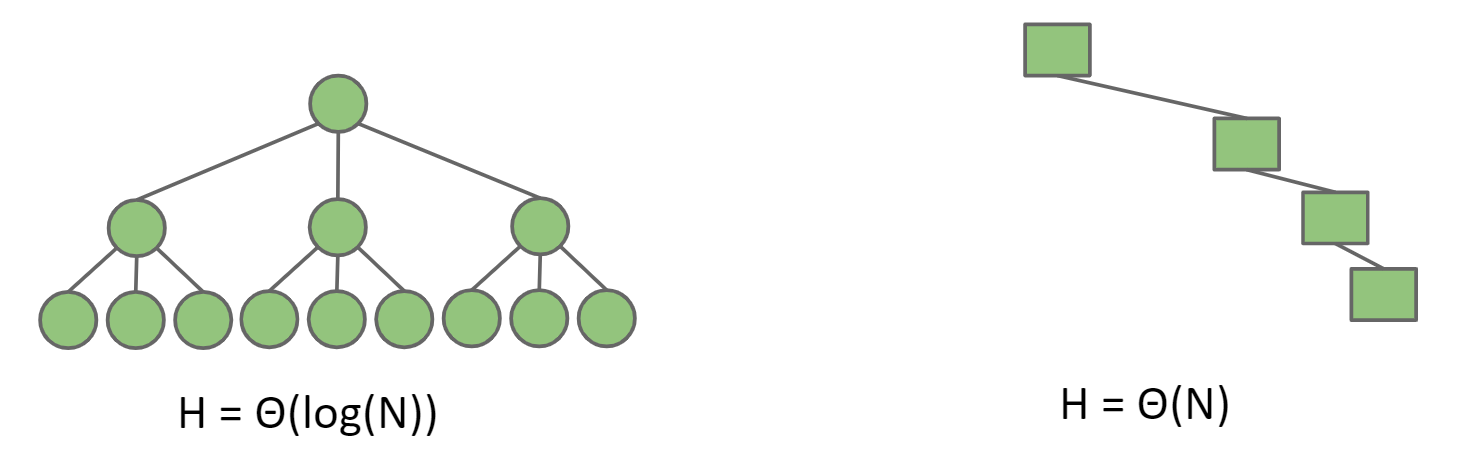
    }
}
```
- 在"bushy tree"的情况下采用level-order进行遍历的复杂度为Θ(N)，其中N为树的总节点数
  因为先考虑最上面一层，visitLevel1次
  考虑第二层，visitLevel1+2=3次
  考虑第三层，visitLevel1+2+4=7次
  因此考虑第logN层，visitLevel$$2^{1} + 2^{2} + 2^{3} + … + 2^{log_2N} - log_2N=\Theta(N)$$
- 在"Spindly tree"的情况下采用level-order进行遍历的复杂度为Θ($N^2$)，因为
  考虑第一层 visitLevel1次
  考虑第二层visitLevel1+1=2次
  考虑第三层visitLevel1+1+1=3次
  考虑第N层visitLevel$$1+2+3+…+N=O(N^2)$$

depth first traversal：先遍历到叶节点

preOrder(BSTNode x) {
    if (x == null) return;
    print(x.key);
    preOrder(x.left);
    preOrder(x.right);
}

采用depth first traversal遍历的复杂度为Θ(N)

QuadTree

两个对象的比较可以不单单是一维的，也可以是二维的，比如a=(1.5,1.6)和b=(1.0,2.8)这两个坐标，从x轴看a>b，但是从y轴看a<b，因此根据不同的参照系可以形成两个tree

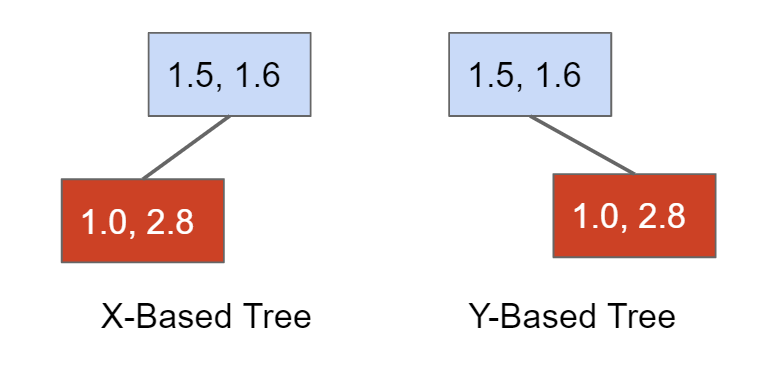
当将这两个tree合并为一个tree是，一个节点实际上根据方向坐标拥有NW、NE、SE、SW四个方向的子节点

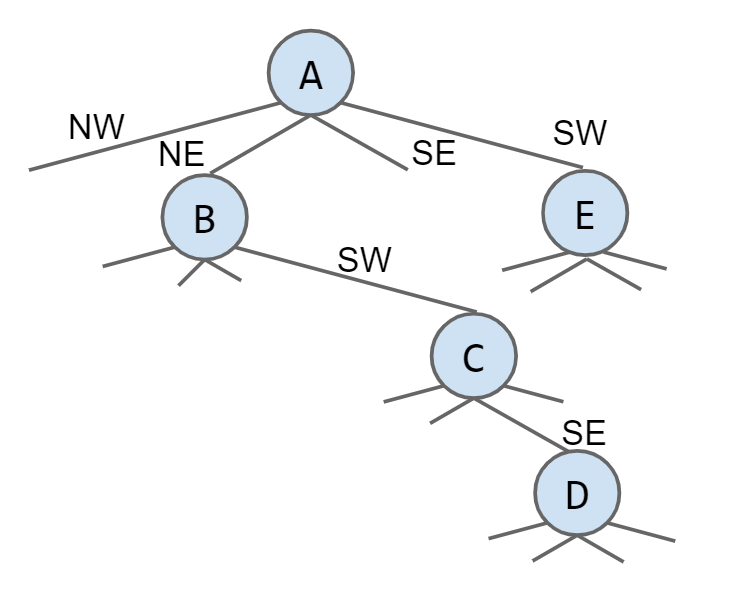
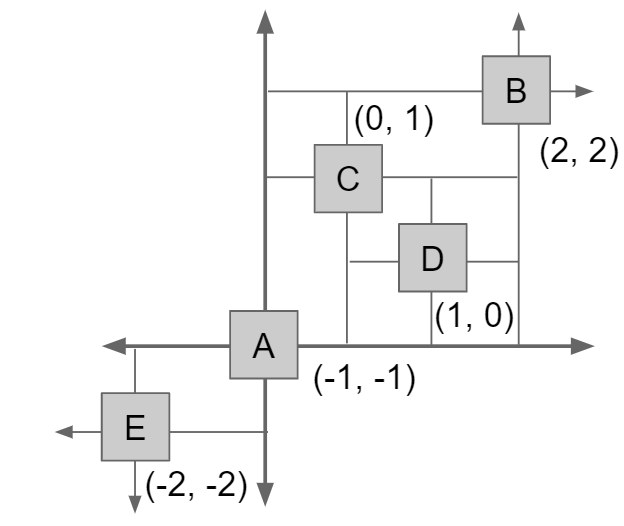
7 Hashing & Heap

7.1 HashTable

Java要求每个Object提供一个hashCode()方法，来将任意的数据转换为index，再通过index查找哈希表实现常数级访问

由于哈希表的大小是有限制的，当需要存储的item的数量大于这个哈希表时，必然会造成多个item存储在一个哈希表的bucket中，我们可以用链表的形式将每个需要存储的对象存储在对应的哈希表位置

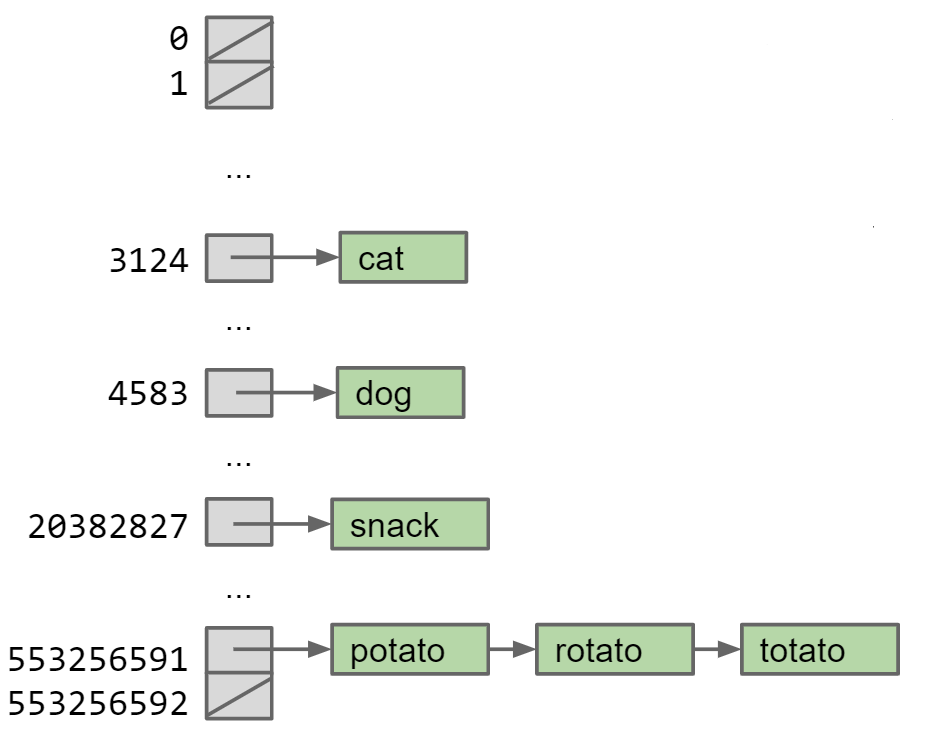
load Factor: 假设M个bucket中需要存储N个item，那么load factor (L) = N / M, 平均的哈希表运算（insert、find）复杂度为Θ(L)

哈希运算的步骤：

计算hashCode: $-2^{31}$到$2^{31}-1$之间
计算index = hashCode floormod M，其中floormod可以进行负数的mod，比如-1 floormod 4 = 3。M为哈希表的bucket数量
如果L = N / M太大，增加M

计算hashCode的方法：

对于String来说，可以用

$$h(s) = s_0 * 32^{n-1} + s_1 * 32^{n-2} + … + s_{n-1}$$

其中$s_n$表示第n个character转化为int的值，比如第n个char为a，则$s_n$为1

但是这种办法会造成一个问题就是当String很大时高位的char都被忽略，因为hashcode是在不断向左移5位的，解决方案是可以将底数从32变成31，这样就会造成位的”混乱“，而这种混乱可以避免上述情况

Java中String对hashCode()方法的实现

public int hashCode() {
    int h = hash;
    if (h == 0 && value.length > 0) {
        char val[] = value;
        
        for (int i = 0; i < value.length; i++) {
            h = 31 * h + val[i];
        }
        hash = h;
    }
    return h;
}

对于递归的数据结构，hashcode也要用递归的方式计算。BST对hashCode()方法的实现

@Override
public int hashCode() {
    if (this.value == null) {
        return 0;
    }
    return this.value.hashCode() + 31 * this.left.hashCode() + 31 * 31 * this.right.hashCode();
}

default hashCode的实现：return this，也就是返回对象的地址，这会造成相同值的对象可能有不同的hashCode，这是我们不想看到的。重写equals方法也需要重写hashCode方法以保证equals的两个该类对象拥有相同的hashCode

HashMap

HashMap实现了Map接口，使用put(key, value)存储对象到HashMap中，使用get(key)从HashMap中获取对象。

当用put()传递键和值时，先对键调用hashCode()方法，根据计算得到的hashCode来计算应该将这个entry放在哈希表的哪一个bucket中，如果这个Bucket中存在一个键.equals()和需要Put的键相等，那么覆盖原先键的value，否则在链表头部插入这个键值对。当负载因子L超出一定的阈值后，将哈希表的索引扩展两倍并进行rehash

7.2 Priority Queue & heap

Priority Queue是一种支持下列API的ADT

/** (Min) Priority Queue: Allowing tracking and removal of the
  * smallest item in a priority queue. */
public interface MinPQ<Item> {
	/** Adds the item to the priority queue. */
	public void add(Item x);
	/** Returns the smallest item in the priority queue. */
	public Item getSmallest();
	/** Removes the smallest item from the priority queue. */
	public Item removeSmallest();
	/** Returns the size of the priority queue. */
	public int size();
}

实现PQ的数据结构：

Binary min-heap，需要有以下性质：

Min-heap指的是每一个node都小于等于其所有的子节点
complete：如果存在缺失的节点，那么缺失的节点只能位于最底一层，所有的节点都要越靠左越好

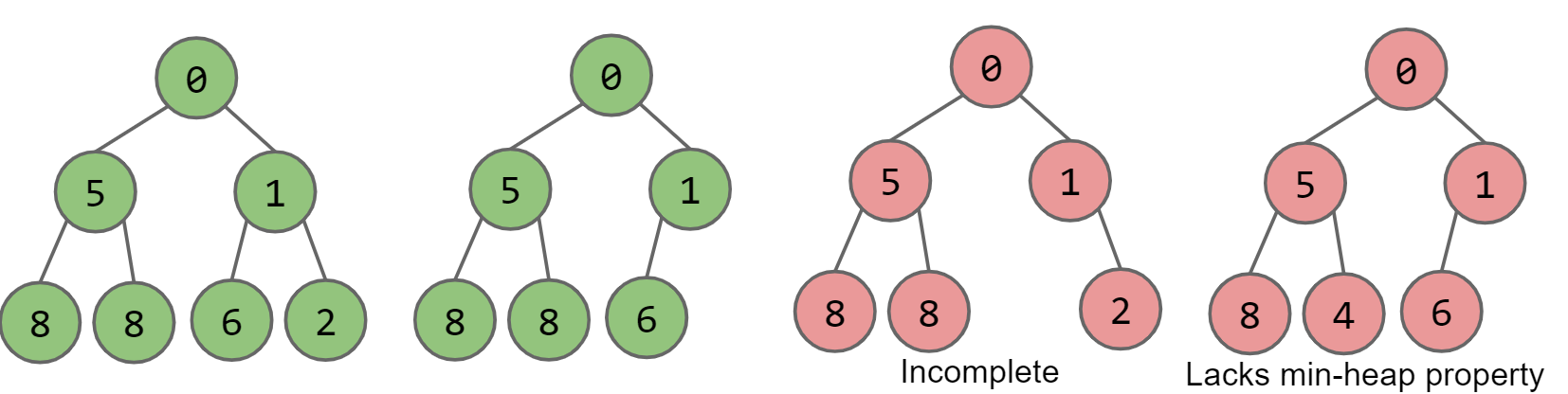
PQ中的getSmallest()只需要返回heap的root节点即可，复杂度为Θ(1)

insert(N)算法：从最底层的最左边的缺失节点开始插入，当插入的节点小于父节点时，调换两者位置，将此步骤进行递归调用，直到满足min-heap条件。

e.g. 向下列heap中插入3

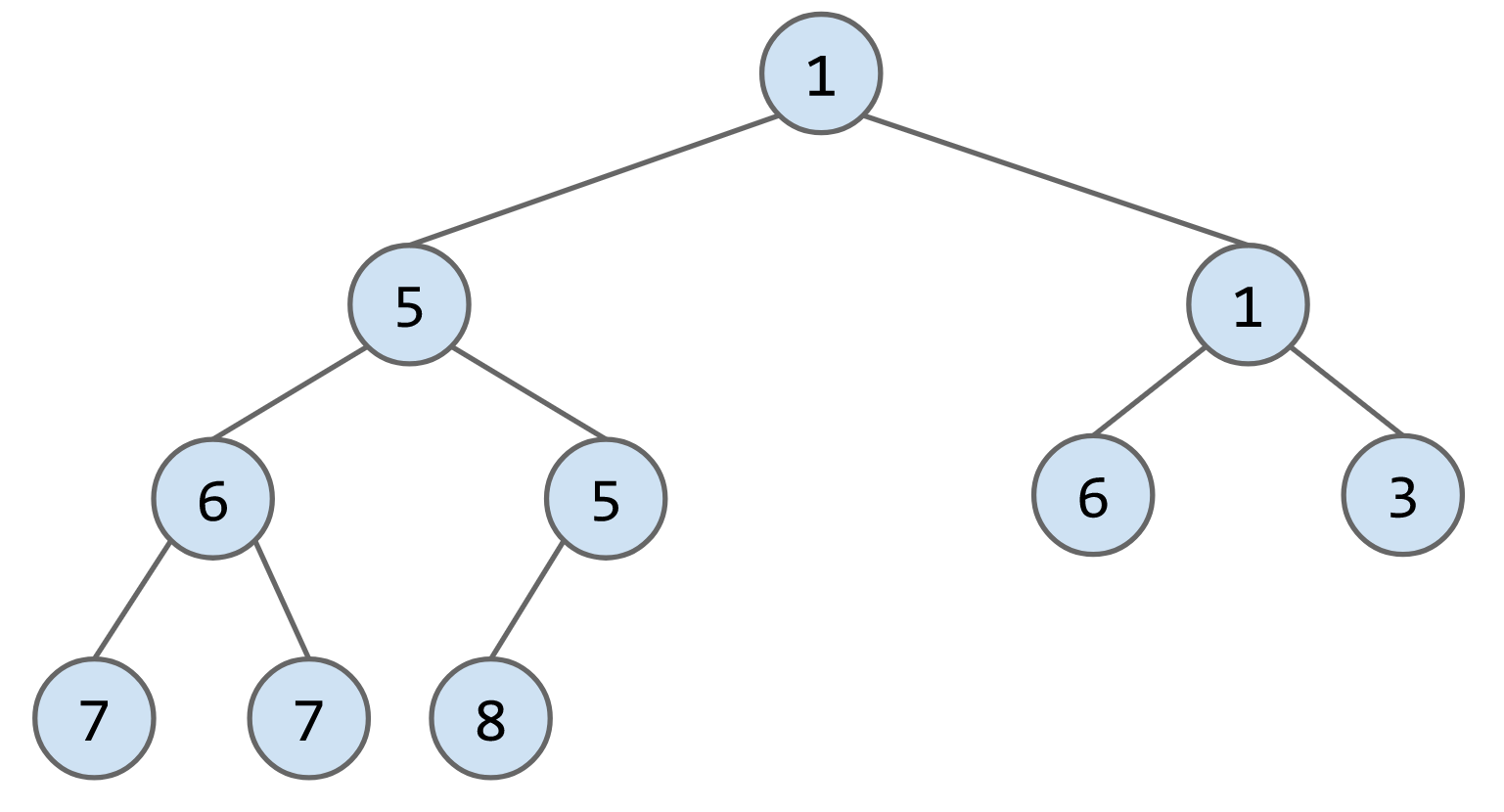
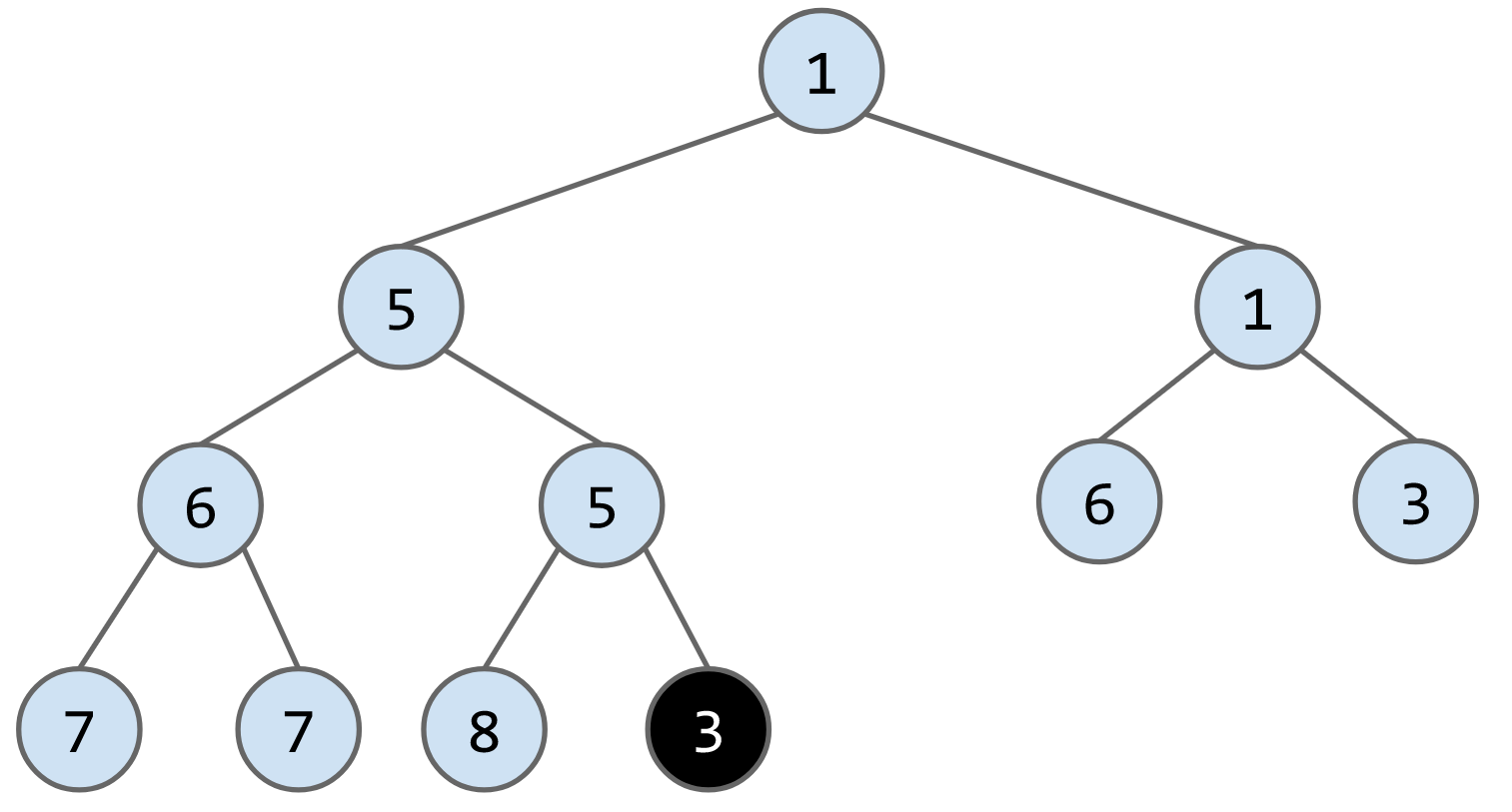
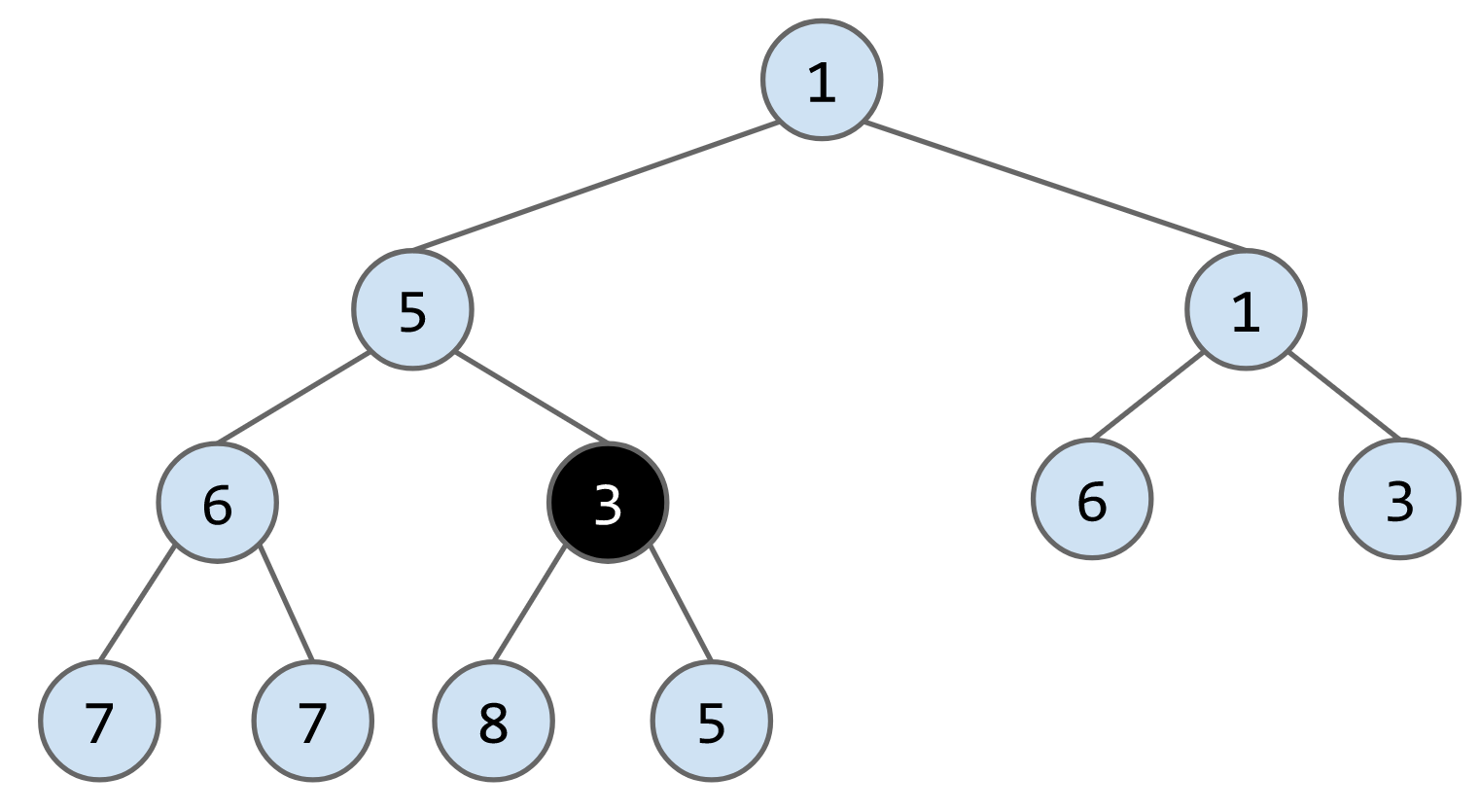
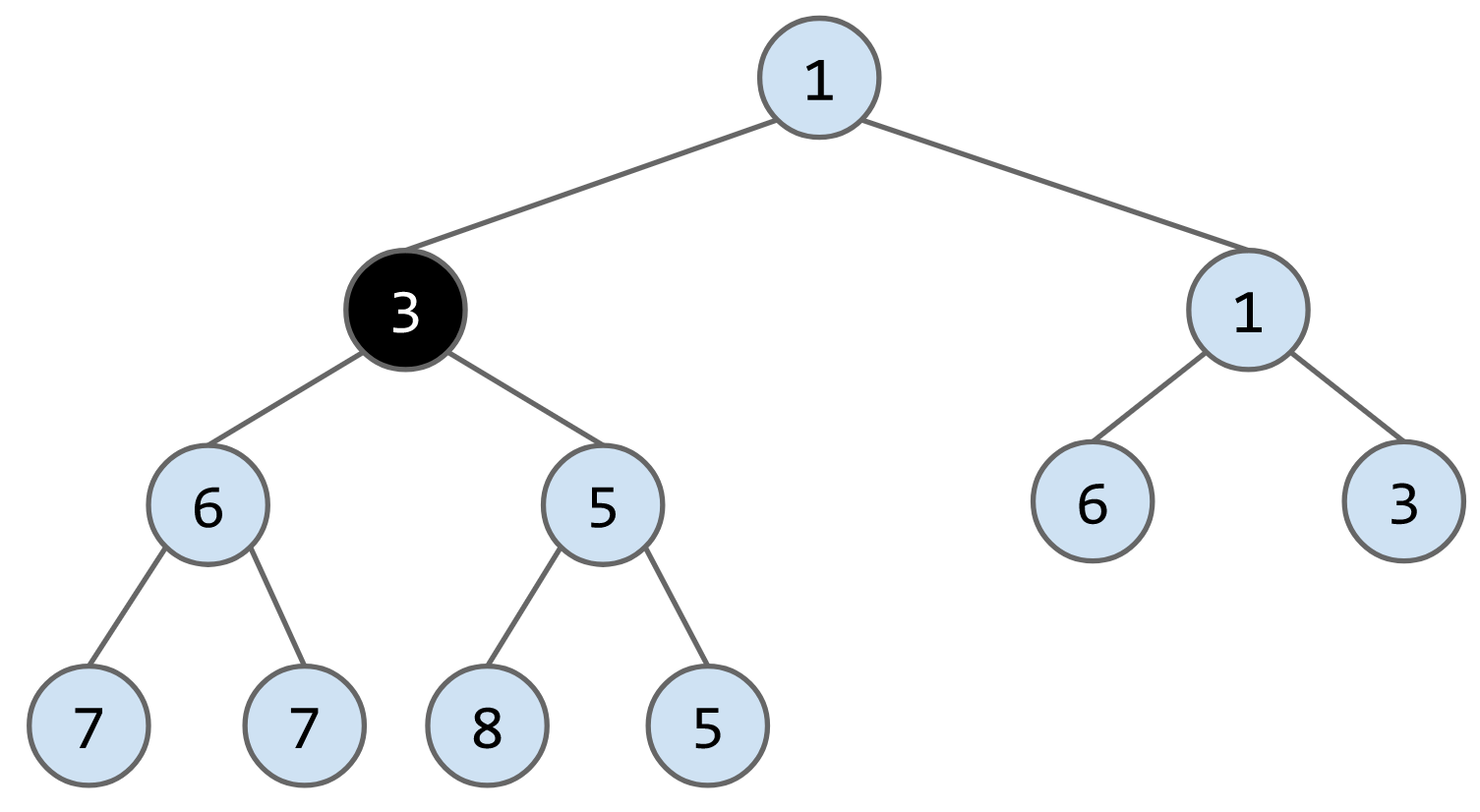
remove()算法：将最后一个节点放到被删除的节点的位子，然后判断其与子节点的大小，如果大于子节点就下放，比如删除下列heap的节点1，将最后一个节点6放到root的位置，最后连续交换节点6的位子

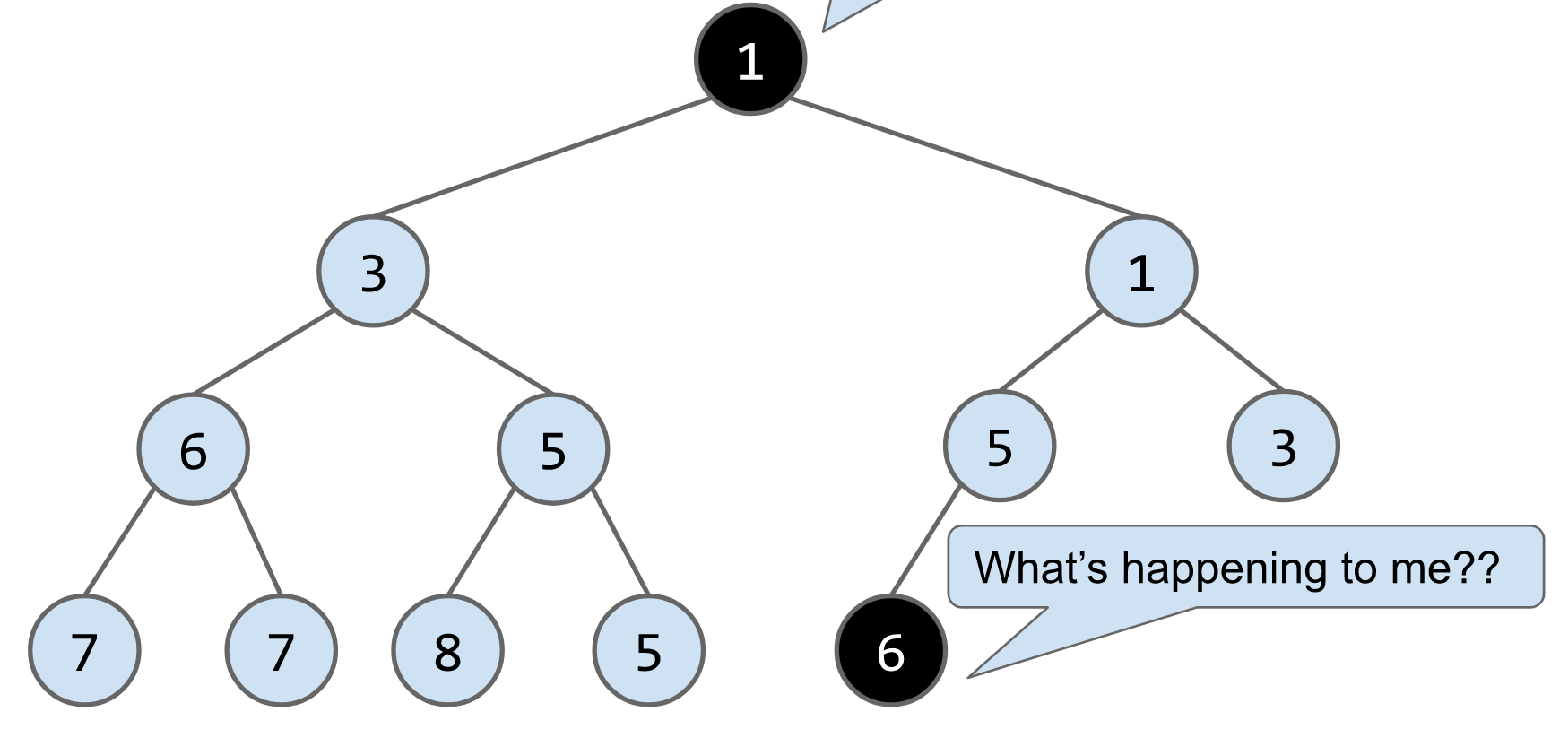
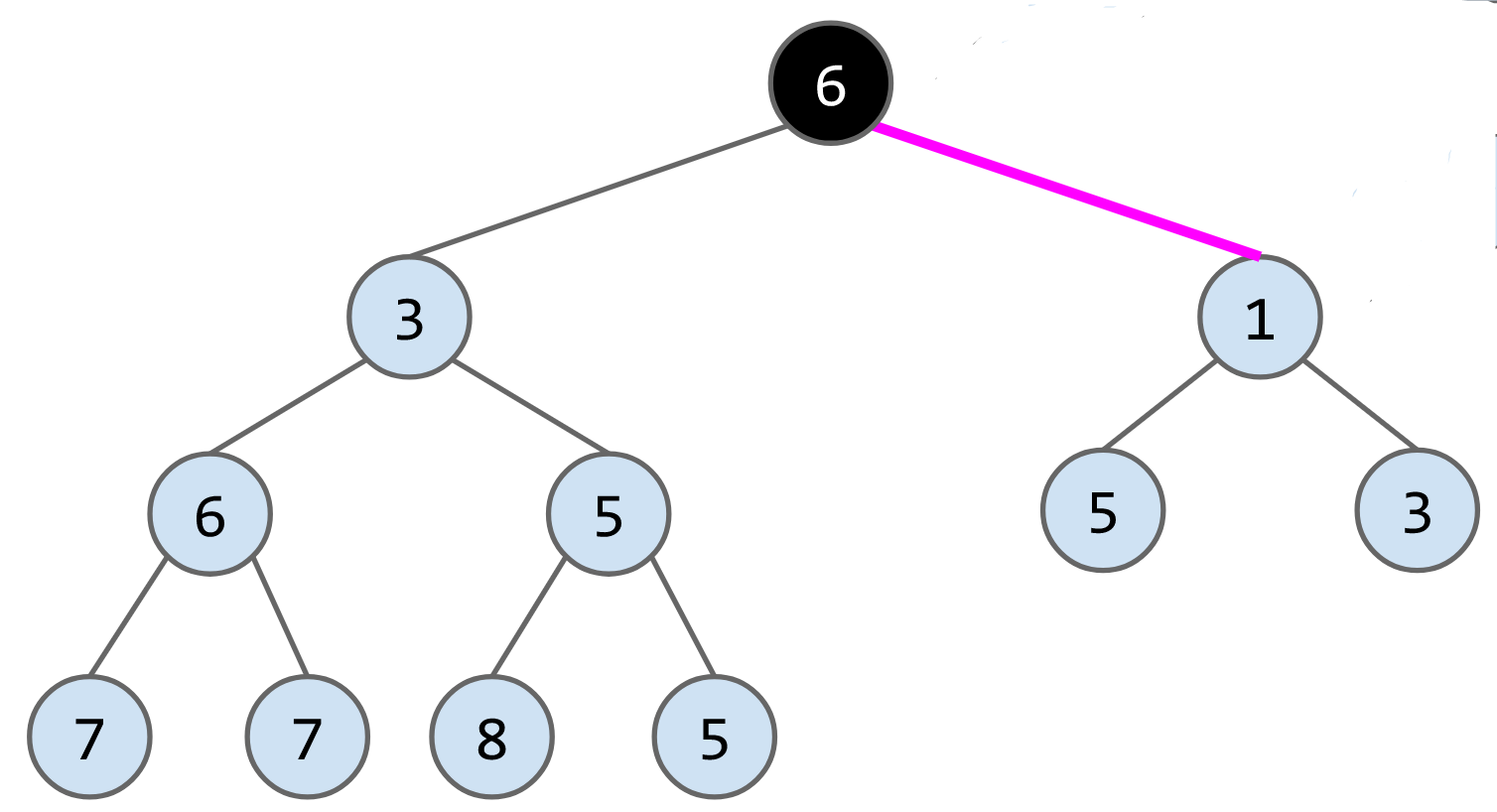
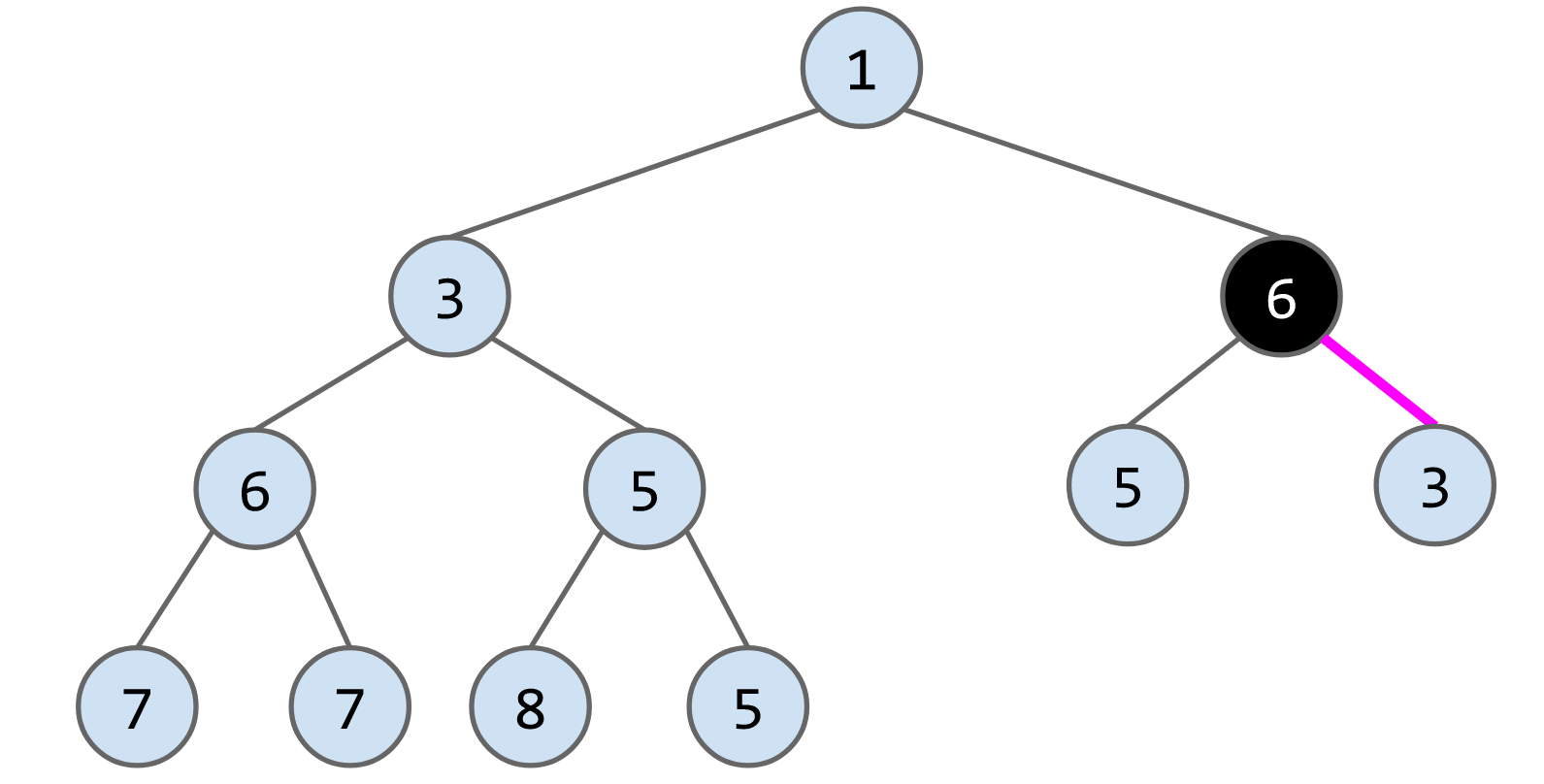
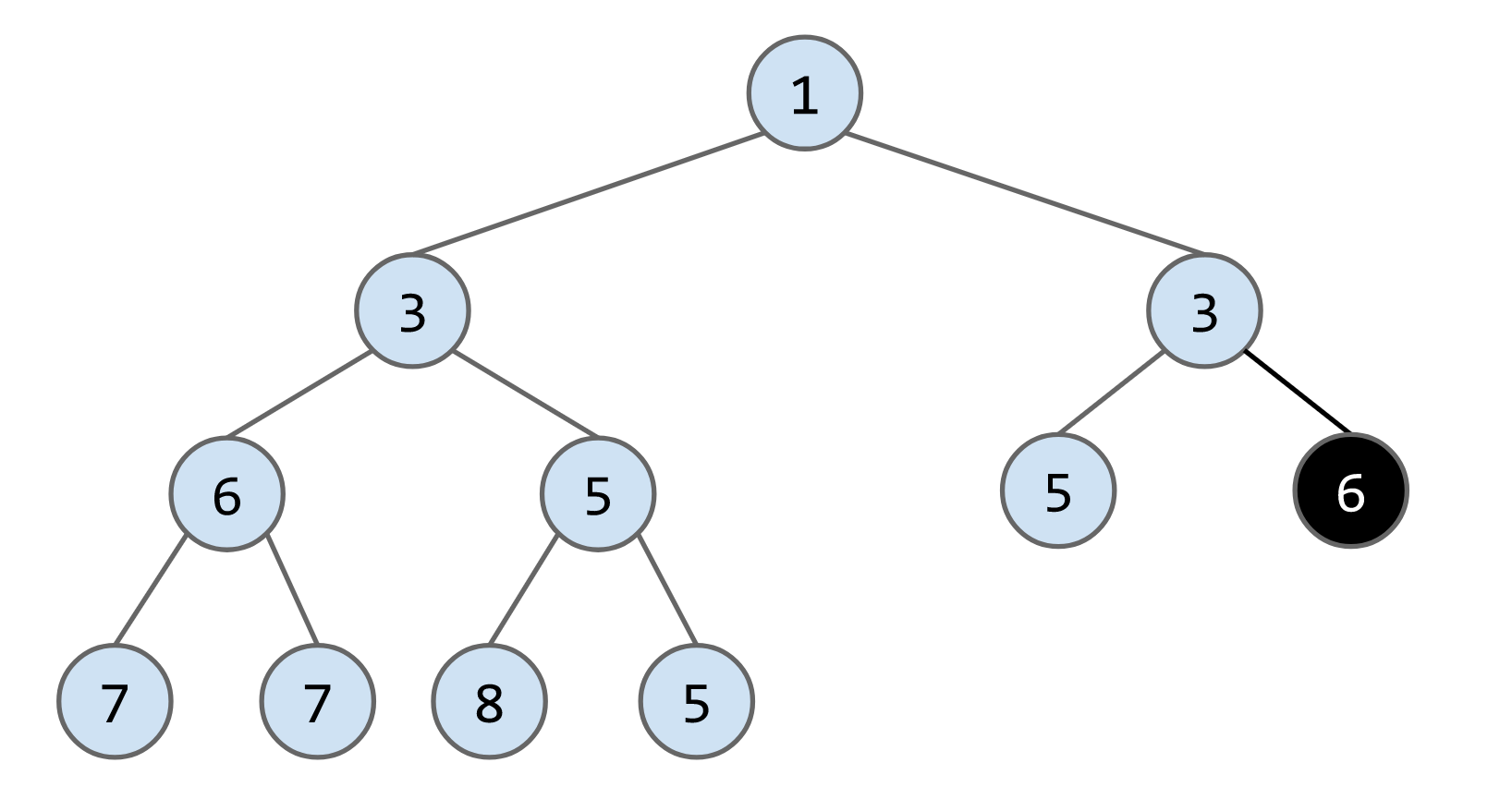
heap implementation

将整个Heap树的所有key按照顺序存放在一个array中，注意要将array[0]的位子空出来，方便parent()和child()的计算

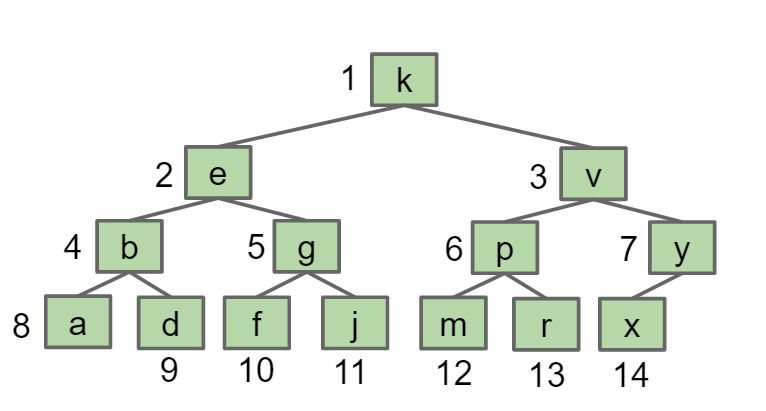
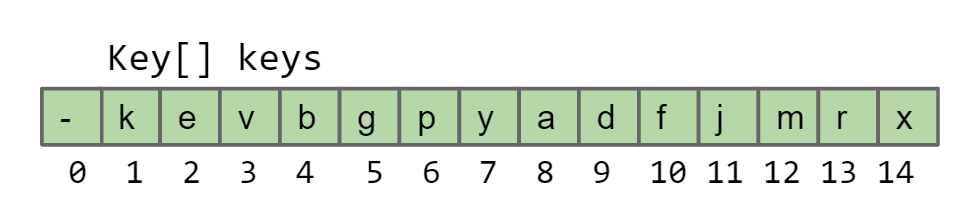
这样可以非常方便地得到计算child和parent的公式

leftChild(k) = k * 2
rightChild(k) = k * 2 + 1
parent(k) = k / 2

/** 最大堆的Java实现，最小堆和最大堆原理一样 */
public class MaxPQ {
    int capacity;  // 堆的最大容量
    int heapSize;  // 堆的大小
    int[] nums;
    
    public MaxPQ(int _capacity) {
        capacity = _capacity;
        heapSize = 0;
        nums = new int[capacity];
    }
    
    // 直接传入一个数组进行原地heapify
    public MaxPQ(int[] _nums) {
        capacity = _nums.length;
        heapSize = capacity;
        nums = _nums;
        buildMaxHeap(nums);
    }
    
    // 插入操作
    public void add(int num) {
        if (heapSize == capacity) {
            nums[heapSize - 1] = num;
        } else {
            nums[heapSize++] = num;
        }
        buildMaxHeap(nums);
    }
    
    // 删除操作
    public int poll() {
        int ret = nums[0];
        // 第一个和最后一个元素进行交换，并减小heapSize
        swap(nums, 0, --heapSize);
        maxHeapify(nums, 0);
    }
    
    // 构建堆
    private void buildMaxHeap(int[] nums) {
        for (int i = nums.length / 2; i >= 0; i--) {
            // 从底层到高层进行heapify
            maxHeapify(nums, i);
        }
    }
    
    // 对一个树进行heapify
    private void maxHeapify(int[] nums, int root) {
        // 左右节点的Index
        int left = 2 * root + 1;
        int right = 2 * root + 2;
        int max = root;
        // 寻找root、left、right中最大的那个节点，将这个节点和root互换
        if (left < heapSize && nums[left] > nums[max]) {
            max = left;
        }
        if (right < heapSize && nums[right] > nums[max]) {
            max = right;
        }
        if (max != root) {
            swap(nums, max, root);
            maxHeapify(nums, max);
        }
    }
    
    // 交换帮助函数
    private void swap(int[] nums, int a, int b) {
        int temp = nums[a];
        nums[a] = nums[b];
        nums[b] = temp;
    }
}

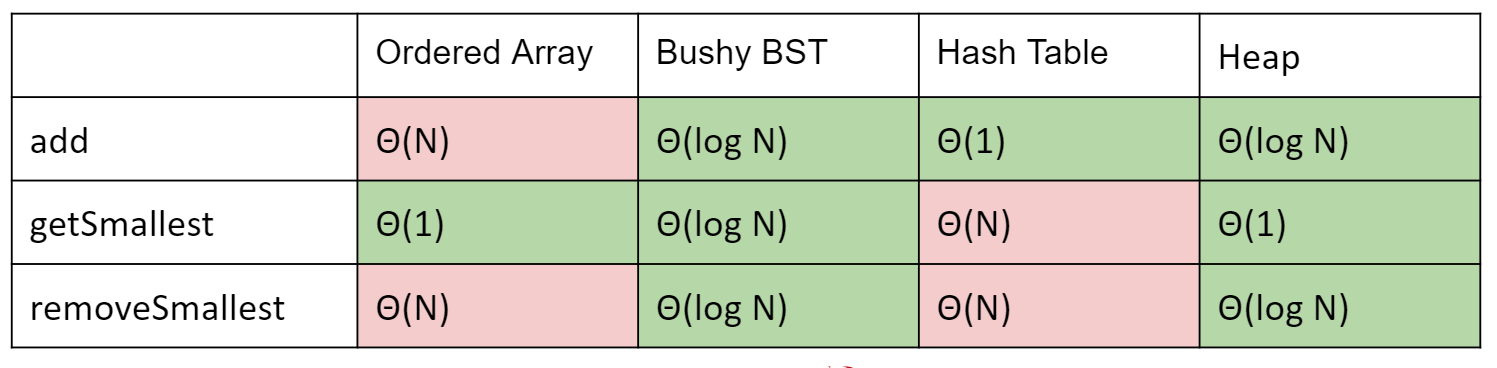
7.3 Data Structure Summary

各种ADT及其实现的数据结构总结

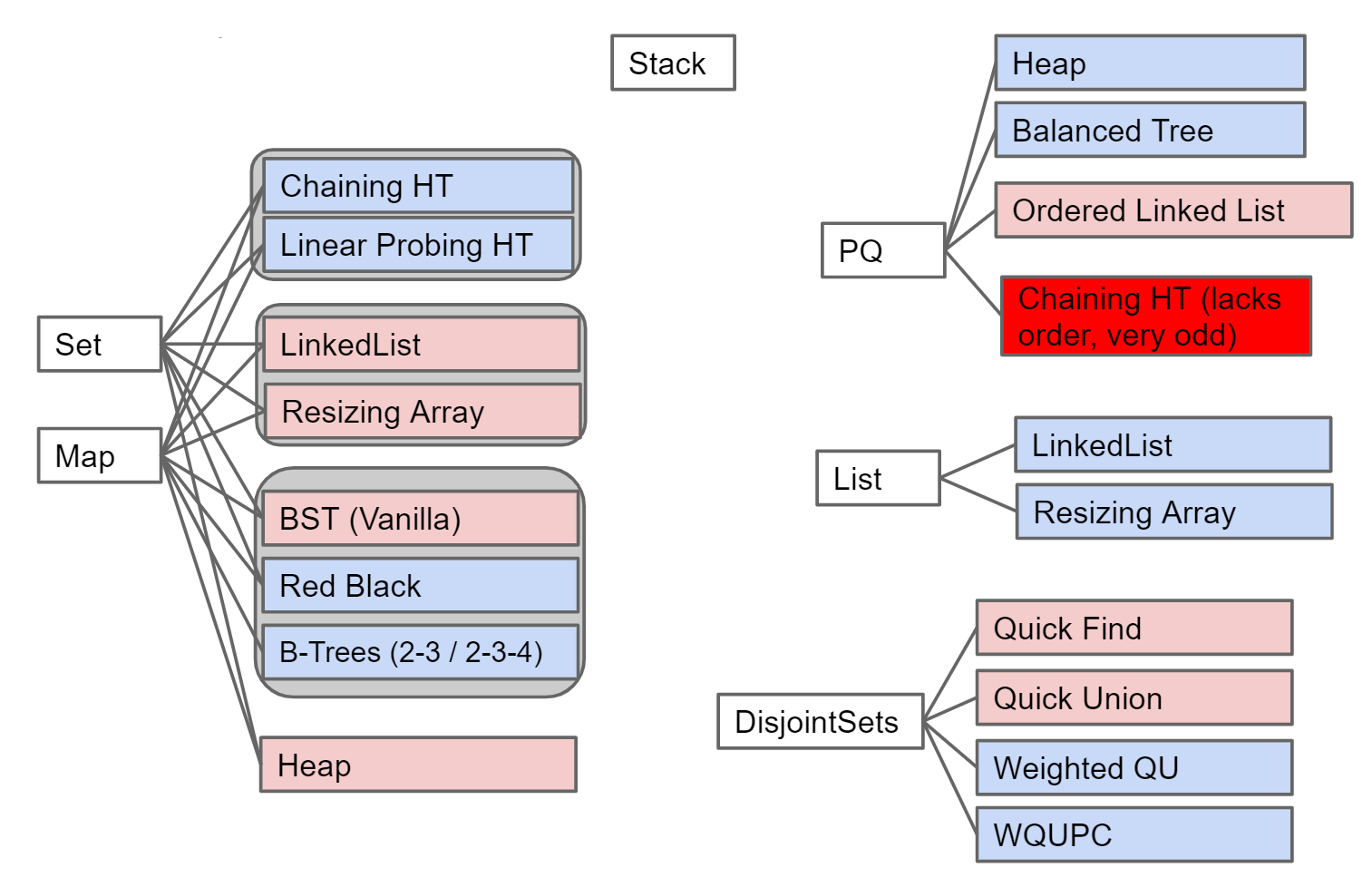
8 Graphs

8.1 Intro to graphs

Graph是一系列被edges连接的vertices/nodes

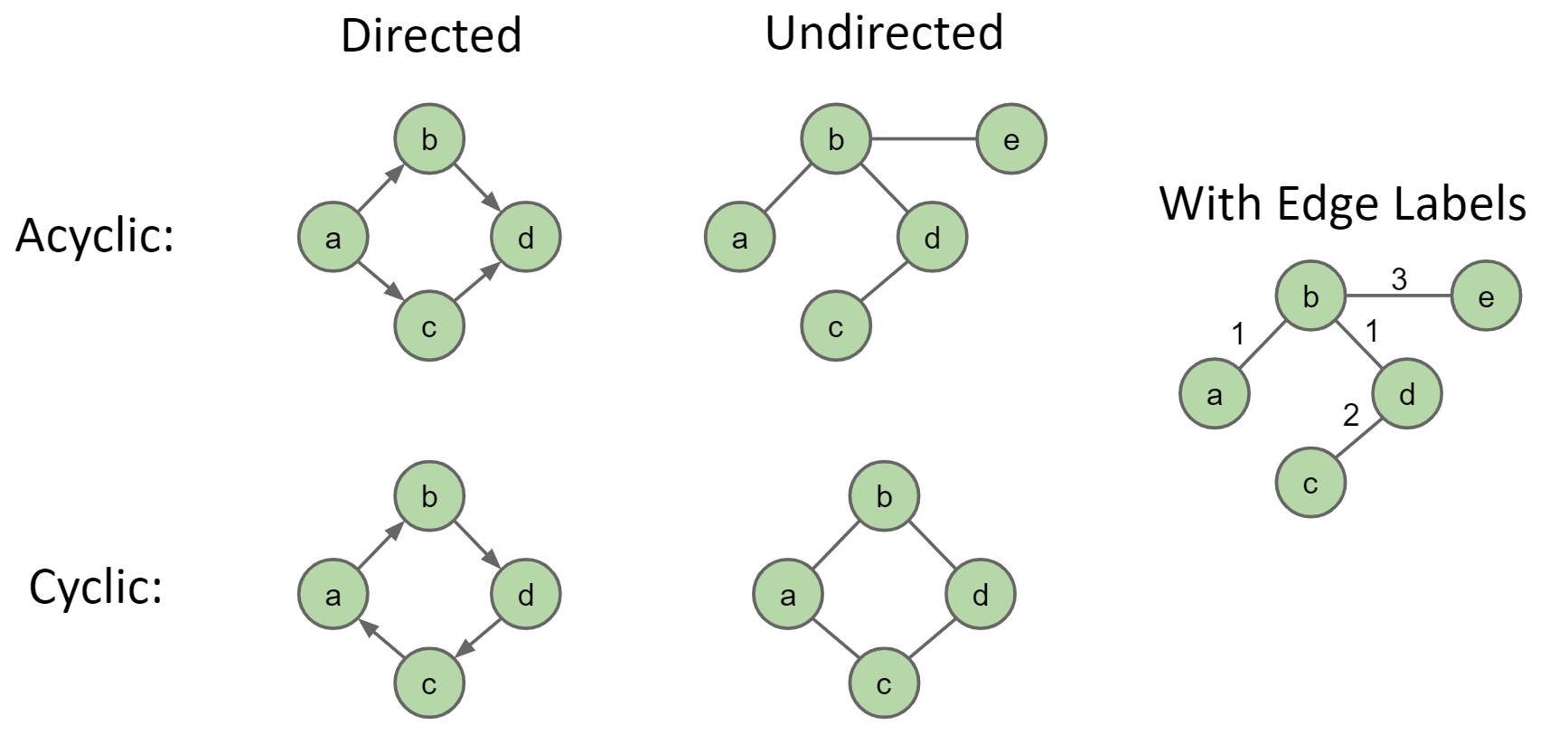
根据链接是否有方向，Graph可以分为directed / undirected

如果directed graph中的一个Node可以沿着一个路径回到自己，则这个graph又是cyclic的，否则就是acyclic。如果一个undirected graph存在多条从一个点到另一个点的路径，则这个graph是cyclic的

Java中的Graph类的API

public class Graph {
    public Graph(int V);  // create empty graph with v vertices
    public void addEdge(int v, int w);   // add an edge v-w
    Iterable<Integer> adj(int v);  // vertices adjacent to v
    int V();  // number of vertices
    int E();  // number of edges
    
    // degree is the # of adjacent vertices connected to some vertex
    public static int degree(Graph G, int v) {
        int degree = 0;
        for (int w : G.adj(v)) {
            degree += 1;
        }
        return degree;
    }
}

8.2 Graph Traversal

Depth first traversal

判断某个节点s到另一个节点t之间是否有一个path：

标记s
如果s==t 返回true
判断所有s的没有被标记的邻近节点是否和t相连，一旦有一个相连就返回true

public class DepthFirstPaths {
    private boolean[] marked;
    private int[] edgeTo;
    private int s;
 	
    public DepthFirstPaths(Graph G, int s) {
        ...
        dfs(G, s);
    }
 	
    private void dfs(Graph G, int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
        if (!marked[w]) {
            edgeTo[w] = v;
            dfs(G, w);
        }        	
    }
}

DFS的时间复杂度为Θ(V+E)，因为查找所有顶点相邻的点所需时间为Θ(E)，而访问所有顶点相邻的点所需时间为Θ(V)

Breadth first traversal

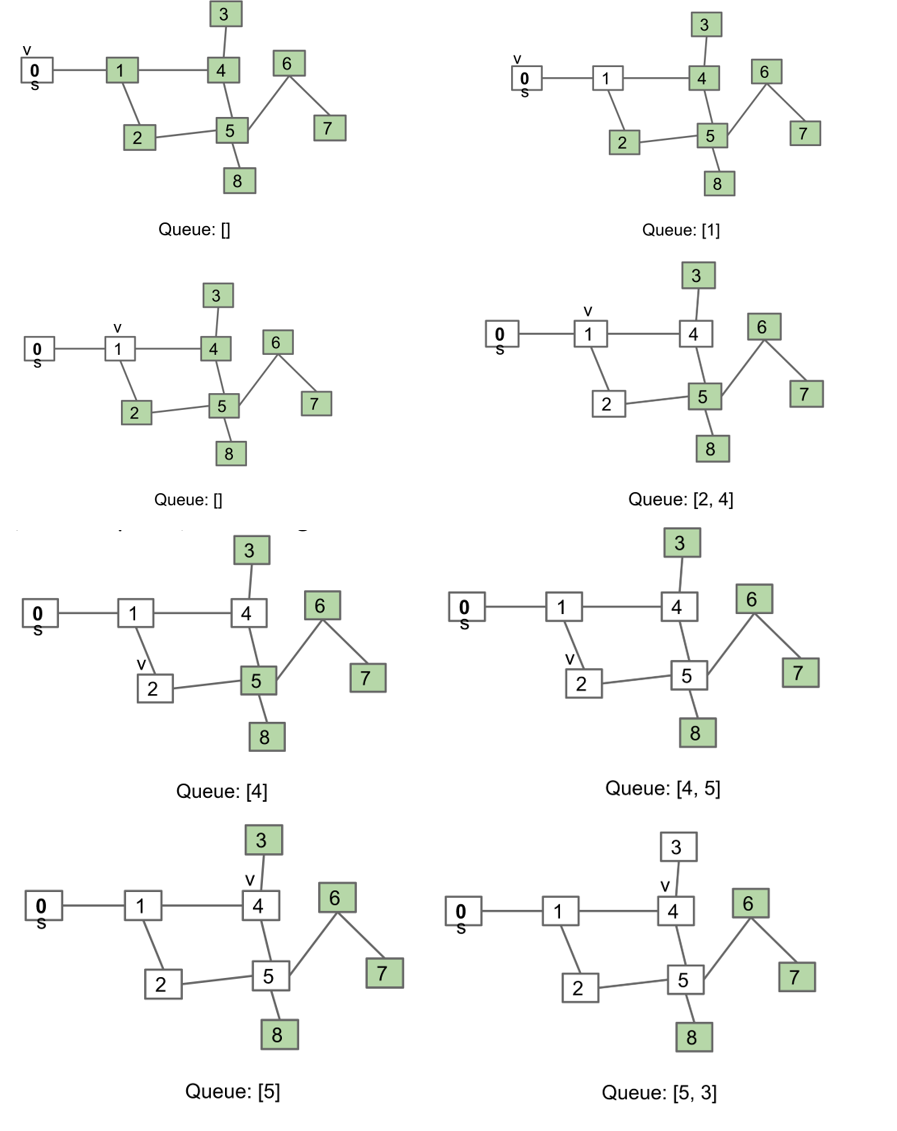
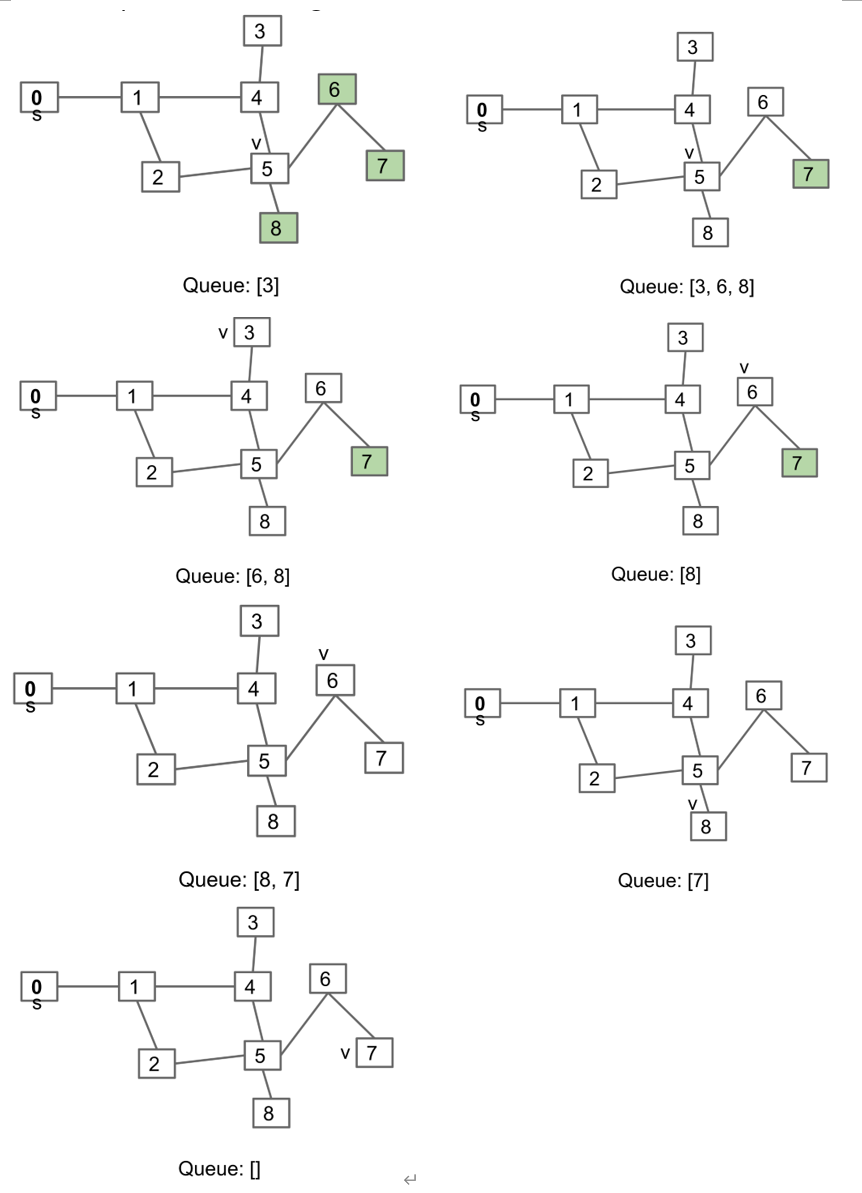
按照从s出发的距离排序

上面的图顺序为012453687

算法：

初始化一个queue，从一个节点s开始，将其加入到queue中，初始化vertex指针v=s，重复2和3直到queue为空
将v从queue中删除
对于所有没有被访问过的v的邻近节点，将其加入到queue中，设置v为queue中的第一个元素

public class BreadthFirstPaths {
  private boolean[] marked;
  private int[] edgeTo;
  ...
	
  private void bfs(Graph G, int s) {
  Queue<Integer> fringe = 
          new Queue<Integer>();
  fringe.enqueue(s);
  marked[s] = true;
  while (!fringe.isEmpty()) {
    int v = fringe.dequeue();
    for (int w : G.adj(v)) {
      if (!marked[w]) {
        fringe.enqueue(w);
        marked[w] = true;
        edgeTo[w] = v;
      }
    }
  }
}

DFS和BFS的区别：BFS用queue(FIFO)来存储fringe，DFS用stack(FILO)来存储/或者使用递归

Topological sort

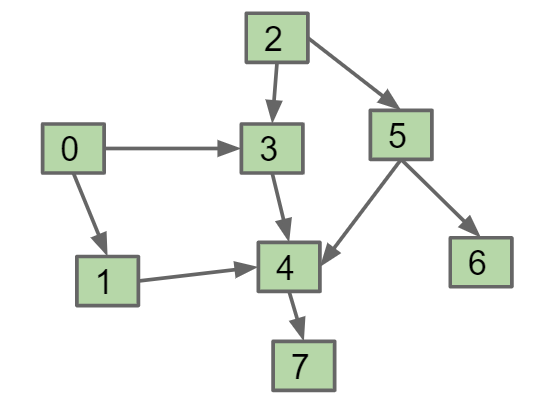
对于有向无环图DAG(Directed Acyclic Graph)，输出一个序列使得当s指向t时，t不能出现在s前面，比如0, 2, 1, 3, 5, 4, 7, 6

算法：从入度(degree)为0的所有节点开始，调用postorder DFS，将输出存在list中然后进行reverse

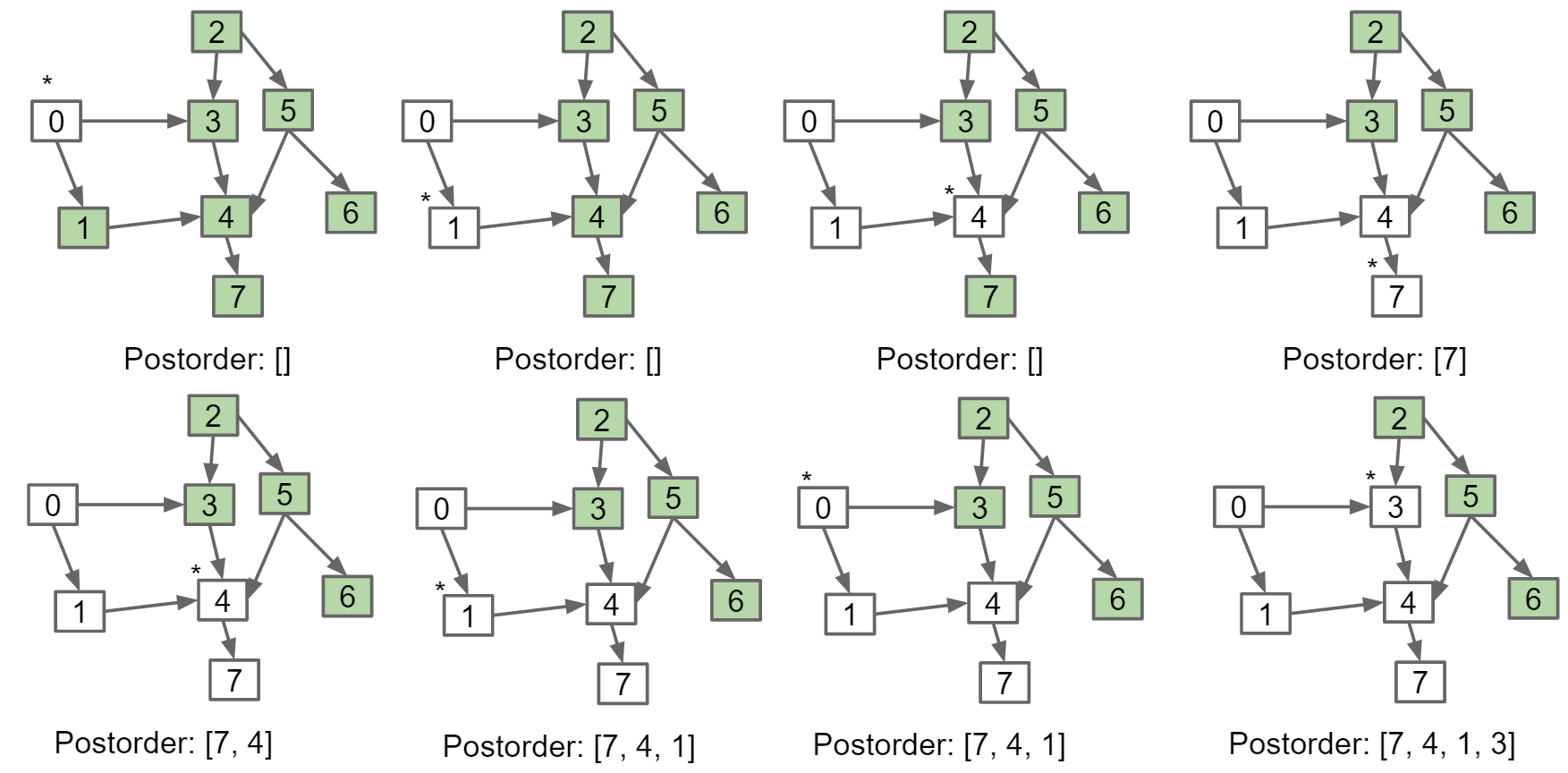
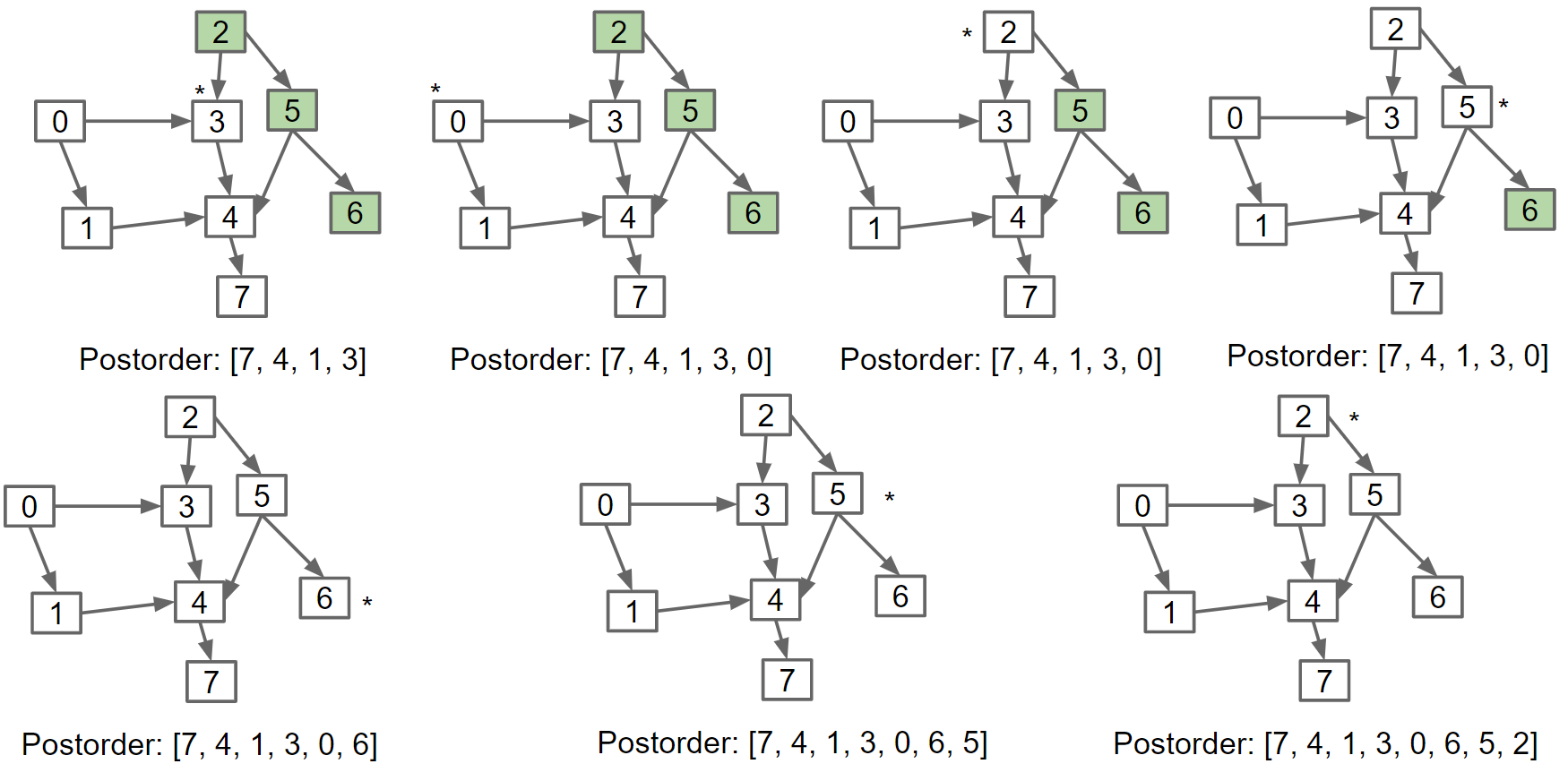
最后结果为[2, 5, 6, 0, 3, 1, 4, 7]

public class DepthFirstOrder {
	private boolean[] marked;
	private Stack<Integer> reversePostorder;
	public DepthFirstOrder(Digraph G) {
   	 reversePostorder = new Stack<Integer>();
   	 marked = new boolean[G.V()];
   	for (int v = 0; v < G.V(); v++) {
       	if (!marked[v]) { dfs(G, v); }
	}
	private void dfs(Digraph G, int v) {
   	    marked[v] = true;
   	    for (int w : G.adj(v)) {
           	if (!marked[w]) { dfs(G, w); } 
         }
         reversePostorder.push(v);
 	}
	public Iterable<Integer> reversePostorder()
	{ return reversePostorder; }
}

8.3 Shortest Paths

对于unweighted edge graph来说，breadth first search可以找到从一点到另外一点的最短路径（因为是按照level排序的）。但是对于weighted edge来说，level并不能完全反映远近，因此需要用Dijkstra算法来计算最短路径

Shorteset Path Tree

从一个点到图上所有其他点的最短路径可以组成一个树，因为到任意一个其他点都一定只有一个父节点

Dijkstra Algorithm

假设source节点为s，节点指针为v，先将s加入minPQ中，保存每个节点到s的距离(toSourceDistance)为$\inf$，s到s的距离为0，重复以下动作：

从minPQ中弹出目前到s距离最短的节点作为v
对于v的所有未访问的邻近节点Node n : v，计算n.toSourceDistance=min(n.toSourceDistance, v.toSourceDistance+edge(n, v))，其中edge(n, v)为n和v之间edge的weight，如果v.toSourceDistance+edge(n, v) < n.toSourceDistance，则将edgeTo(n)设置为v
将v设置为已访问，将n加入minPQ中

最后从终点根据edgeTo回溯到起点即可

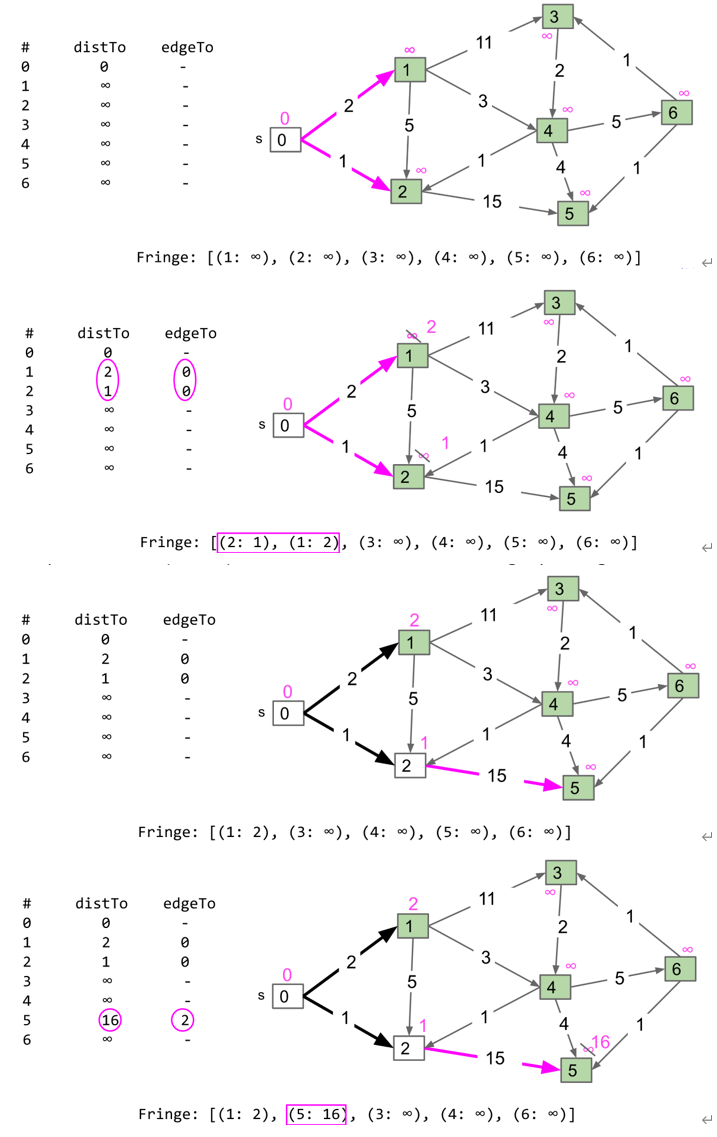
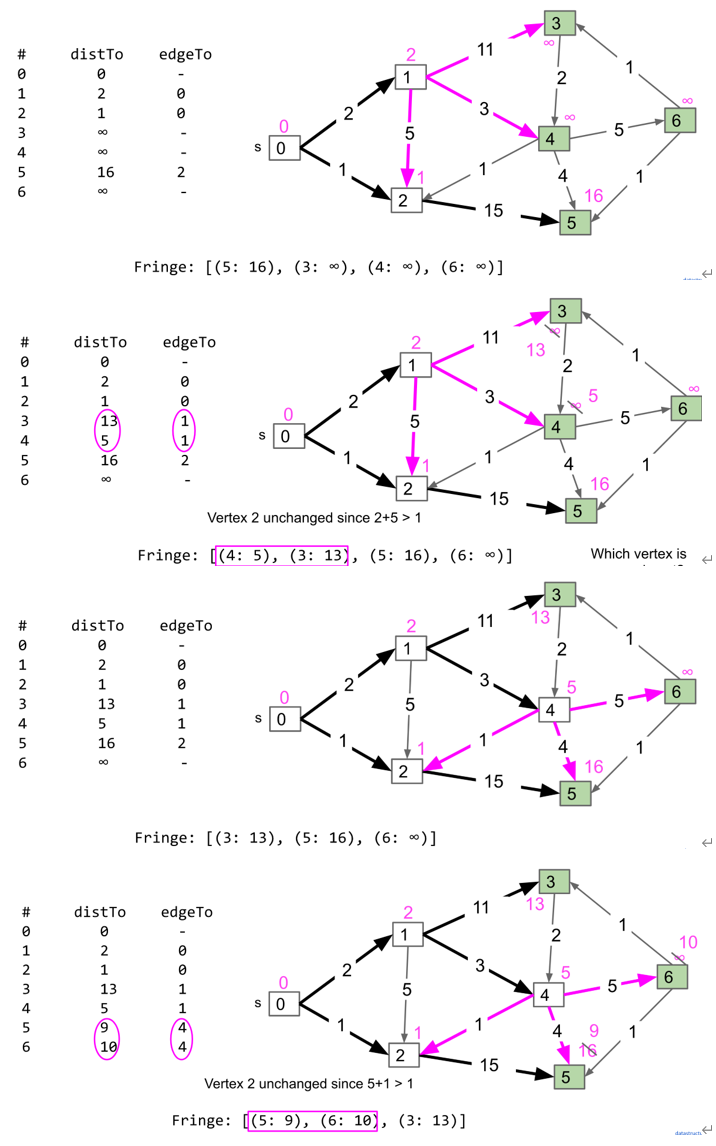
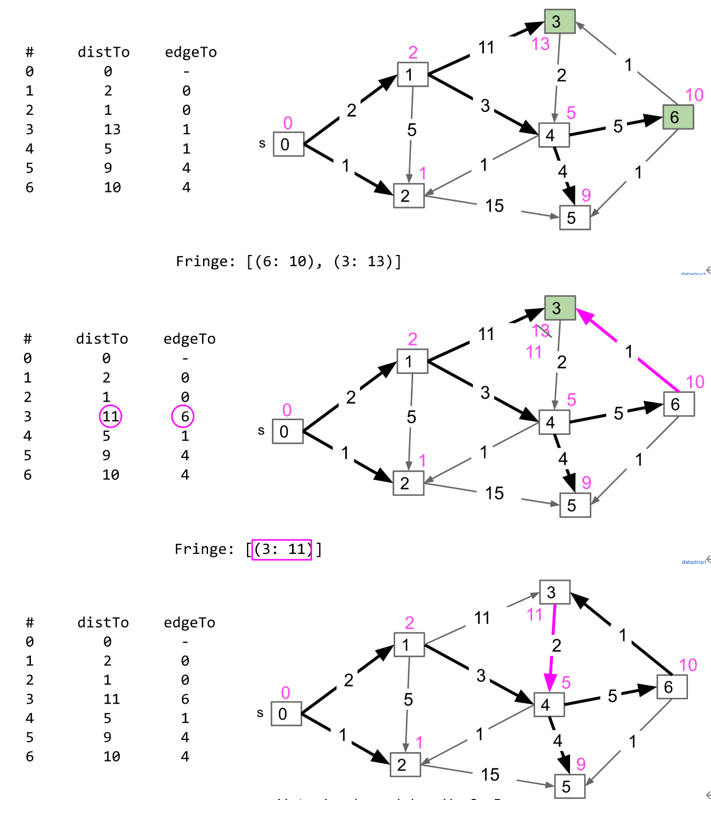
A*算法

A*算法适用于已知目的地的情况而不是对所有点查找最短路径

与Dijkstra的best first不同，Dijkstra在将v从minPQ中pop出来的依据只有该点到source的距离，但是A*考虑了该点到source的距离+该点到目标点的估计距离，以此为依据判断pop的先后顺序

这个估计距离不能大于实际距离

但是注意：在更新distTo数列时，依然按照该点到source的距离为依据进行更新，且当访问到目标点时不能够立即停止访问，需要还保证所有目标点的相邻点都已经被访问才能够确定最短路径。这是因为在考虑估计距离的情况下，已经pop出来的节点并不一定位于最短距离的路径中，需要比较所有能够访问到目标点t的最短路径才可以。

可以参考Project 3: BearMap中用A*算法实现的Router

https://github.com/tommyfan34/cs61b/blob/main/proj3/src/main/java/Router.java

8.4 Spanning Tree

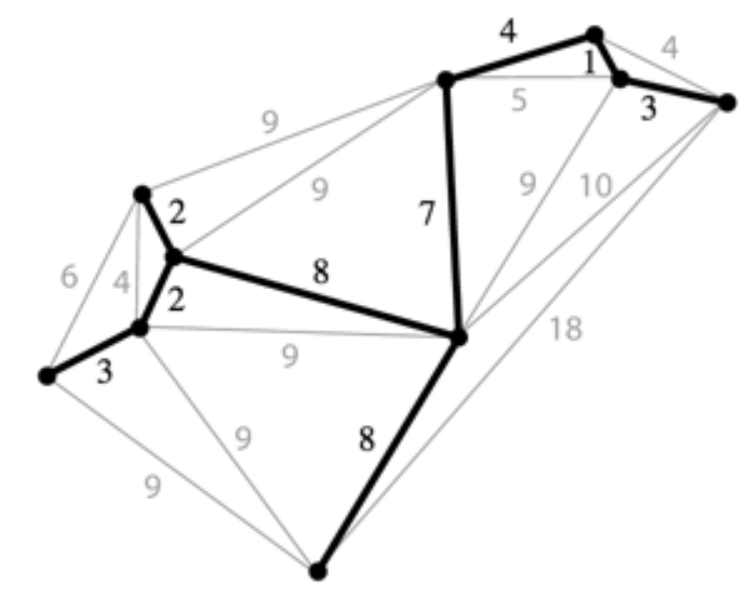
生成树T满足以下条件：

是G的子图
是connected
是acyclic
包含G的所有节点

Minimum Spanning Tree (MST): 在所有可能的生成树中拥有最小的edge weight sum

cut property

将一个图中所有的节点任意分为2部分，比如下图中的灰色节点和白色节点

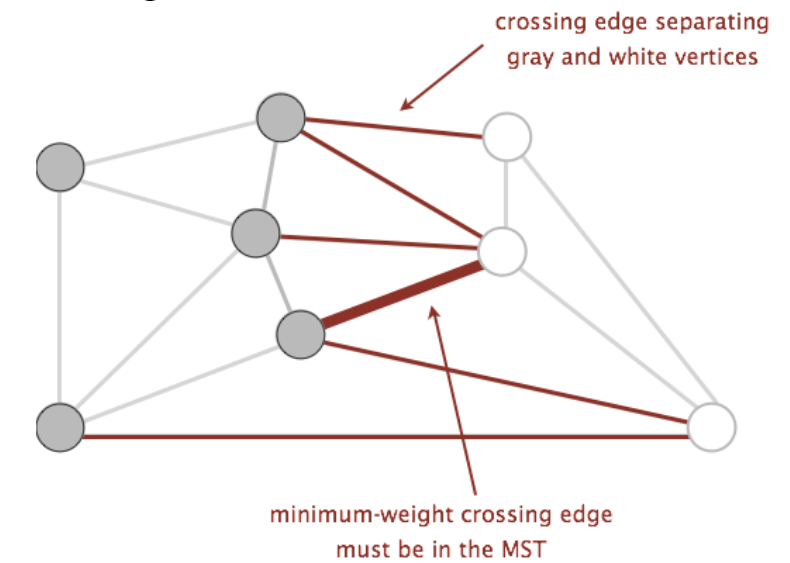
crossing edge是所有连接两种set节点的edge，上图中的红色edge

在所有crossing edge中，weight最小的那个edge一定在MST中

Prim’s Algorithm

这是用来计算MST的算法，基于cut property

先从任意一个node开始，这个node和剩下的node形成了2个set，将这两个set之间的cut edge中weight最小的那个加入到MST中，并且被连接的那个Node加入到MST的node set中，然后继续寻找weight最小的cut edge

和Dijkstra算法很像，但是区别在于Dijkstra中每个minPQ中节点对应的priority是到source的距离，而Prim中每个minPQ中节点对应的priority是和MST节点set之间的cut edge的最小距离（如果不和MST set相连，则priority为$\inf$。

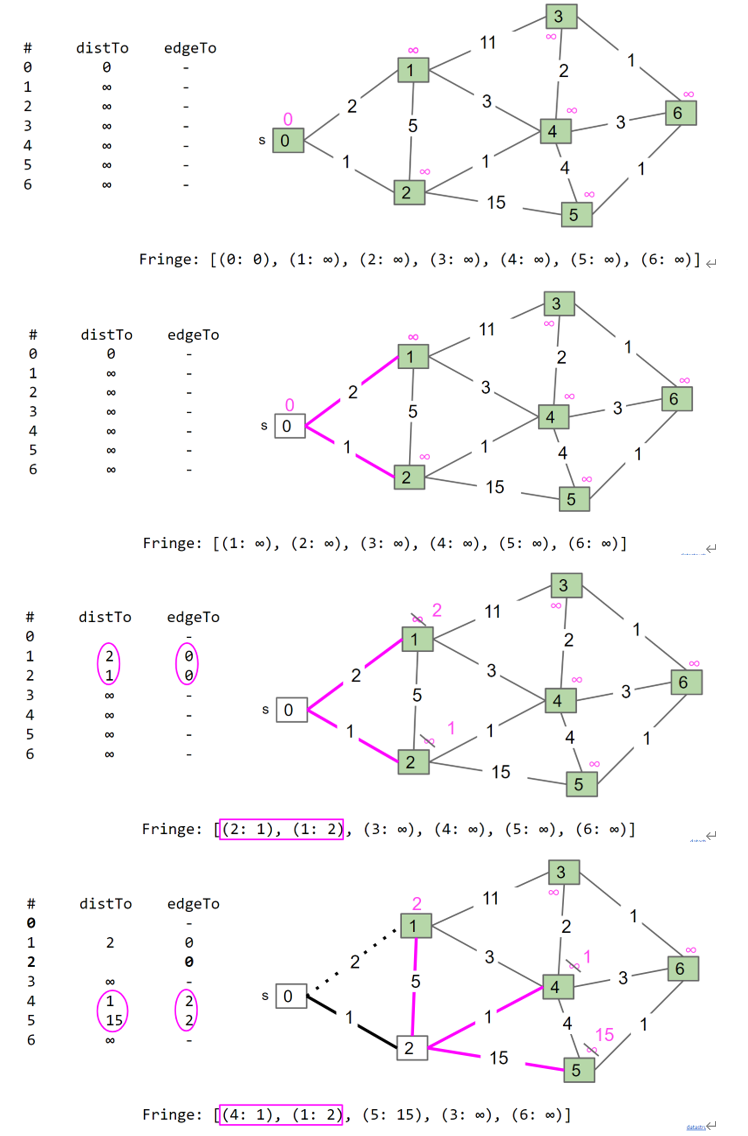
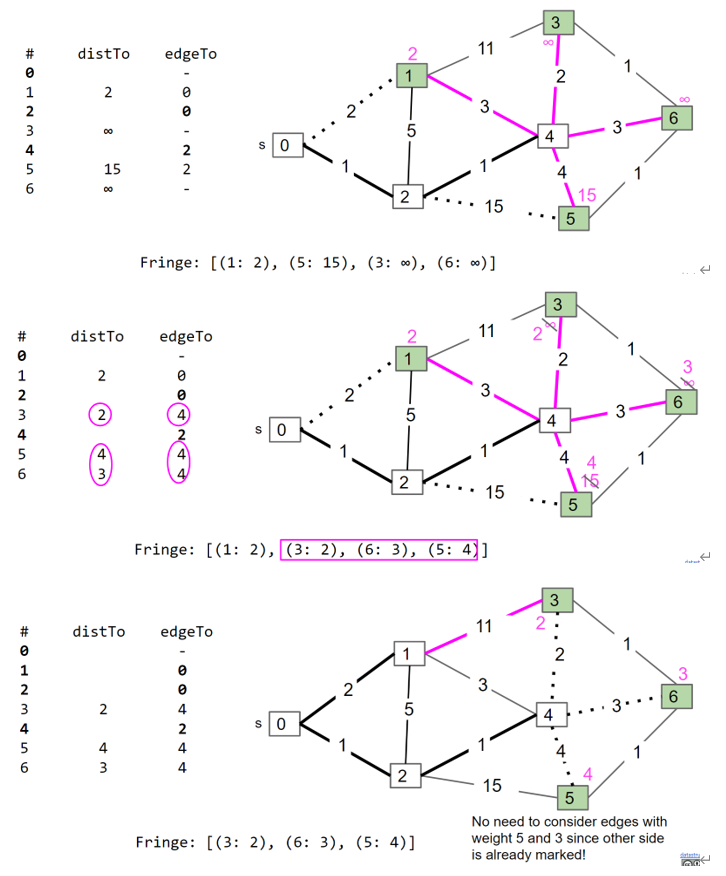
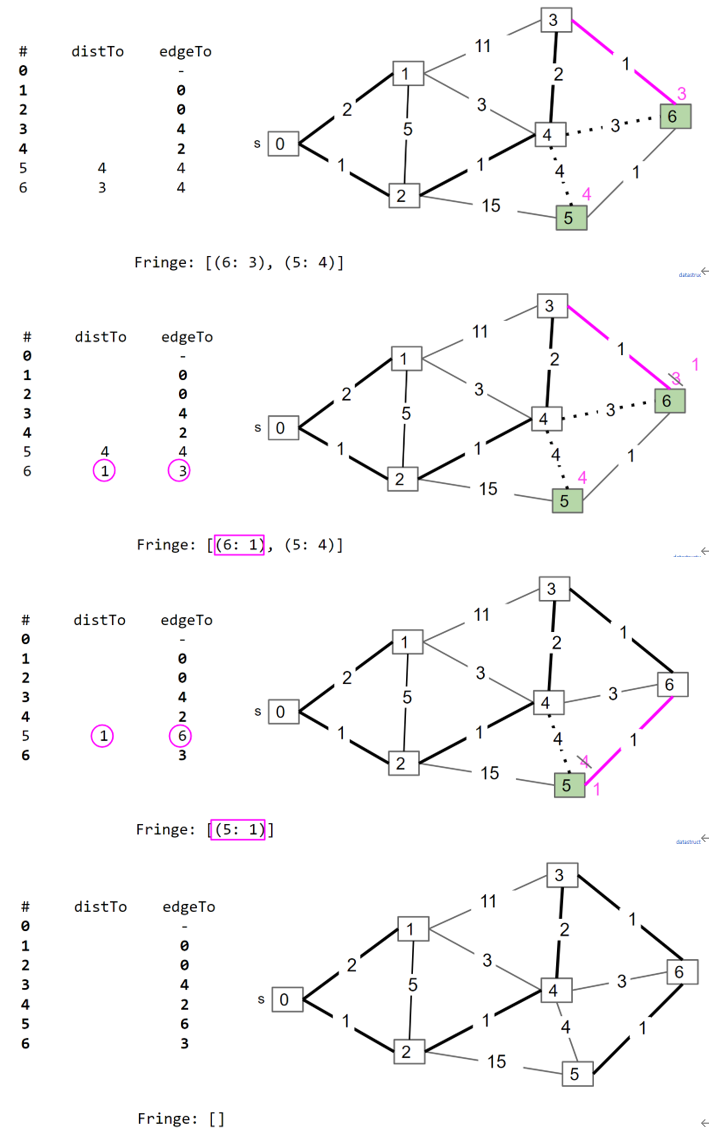
Kruskal Algorithm

将所有edge加入到MinPQ中，从minPQ中依次pop一个edge e，判断如果将e加入到当前的MST中是否会出现cycle，如果不会出现cycle，就将其加入到MST中，重复上述步骤直到加入了V-1个edge为止

9 Sorting Algorithm

9.1 Basic Sorting Algorithms

Selection Sort

在array中unsorted部分中找到最小的Item
将这个Item放到sorted部分的最后
继续对接下来unsorted的部分进行selection sort

复杂度$\Theta(N^2)$

Heap sort

与selection sort基本一样，但是将array放到了priority queue中

复杂度$\Theta(NlogN)$

可以将整个输入array作为一个heap，实现in-place heap sort从而不需要另外一个heap，以节约空间

heapfication

从后往前，进行sink(k)，即判断child(k)是否大于自己，是则进行交换

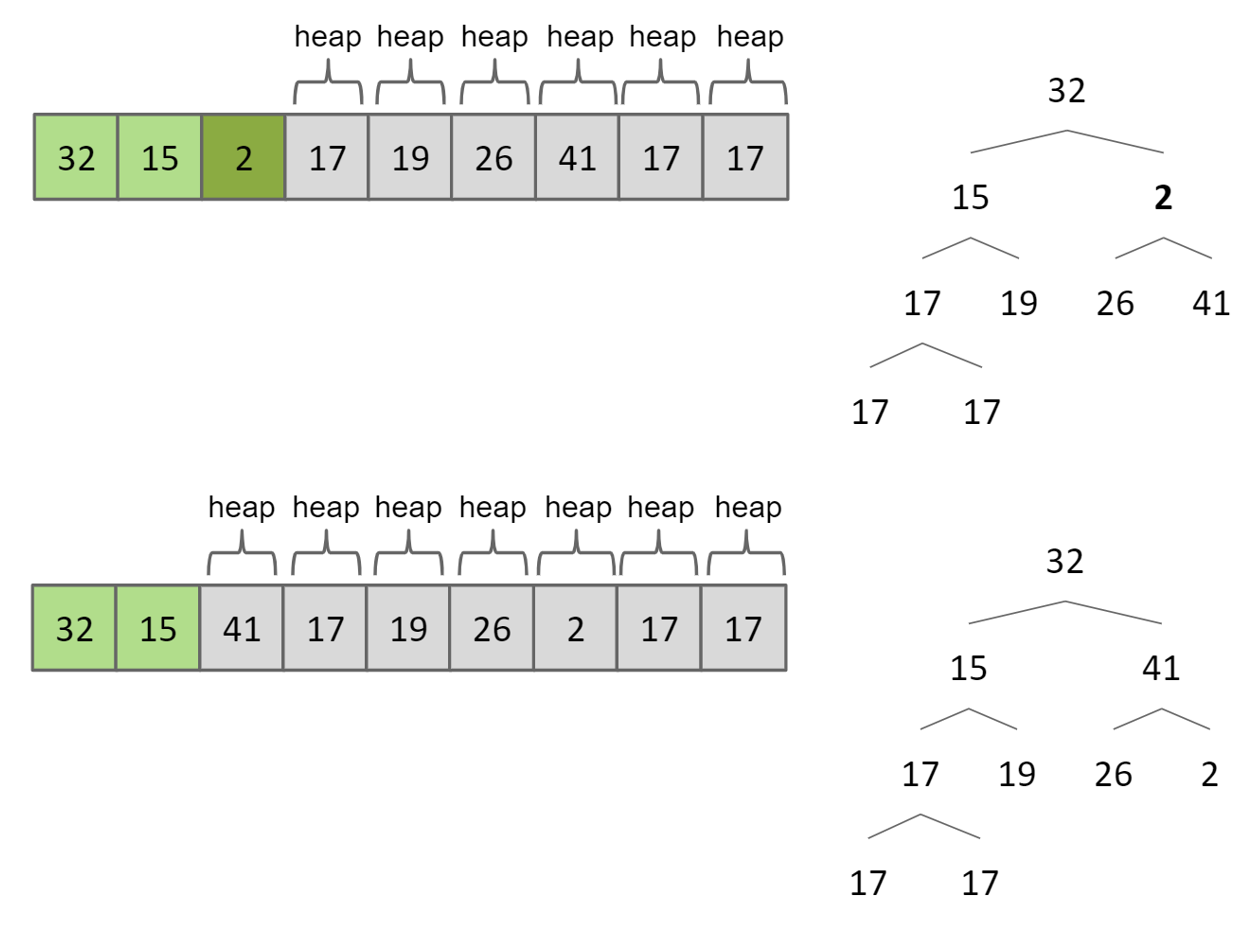
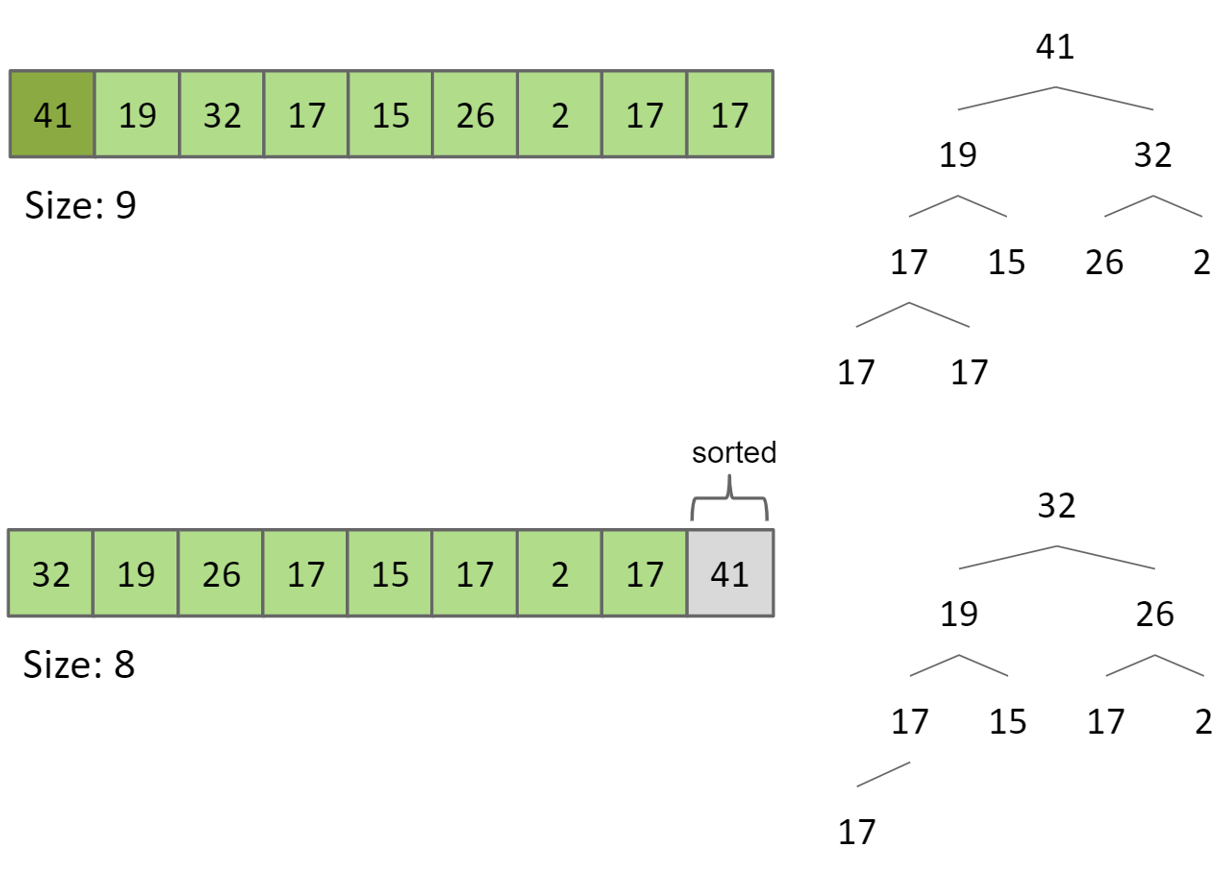
将heap中最大的item删除，放到array中最后一个中去（和最后一个交换，然后最后一个不断进行sink)，重复N次

merge sort

将一个array分成2个，分别对他们进行sort，然后进行merge，merge的方法是不断判断两个sorted array的front pointer指向的数，将较小的那个放到新的array中，并移动相应的那个sorted array的front pointer

可以将array继续分为2个，直到不能再分，此时merge sort的时间复杂度为$\Theta(NlogN)$

Insertion sort

从array的第一个开始将其抽出，插入到新array的正确位置使得新array按顺序排列

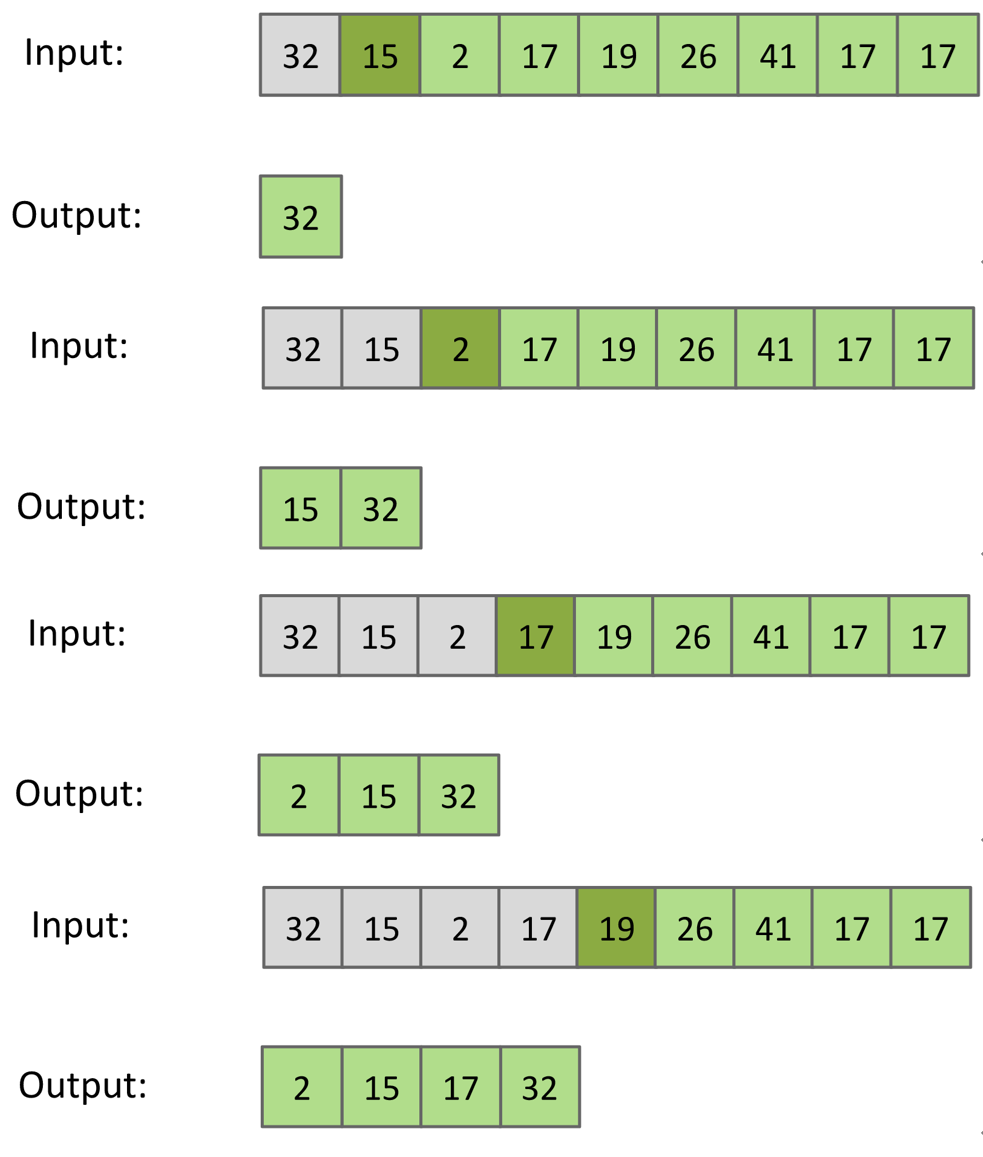
insertion sort的复杂度$O(N^2)$

但是对于一个几乎已经全部sorted array，insertion sort的复杂度为$\Theta(N)$

9.2 Quick Sort

Partition

将一个array以a[j]为界分为2部分，左边的所有元素都小于a[j]，右边的所有元素都大于a[j]

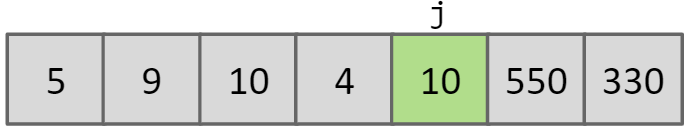
进行Partition的方法：

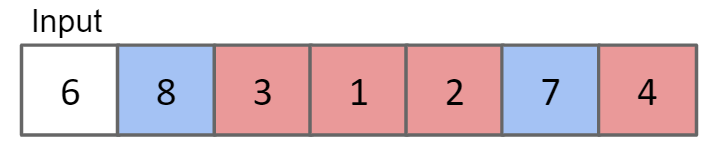
对于input，先扫描一遍蓝色块（大于白色块的），放到新array的最后面，再扫描白色块（array中的第一个），放到新array的蓝色块的前面，最后扫描红色块，放到新array的最前面

partition时间复杂度为$$\Theta(N)$$

可以观察到，经过partition之后array的第一个元素已经被放在了正确的位置，只需要对partition之后的这个元素的左边和右边的sub array继续进行partition即可

quick sort的最好情况（每个pivot都在array的中间）时间复杂度为$$\Theta(N logN)$$

quick sort的最差情况（每个pivot都放到array的两端）时间复杂度为$$\Theta(N^2)$$

quick sort的平均情况时间复杂度为$$\Theta(NlogN)$$

// 快速排序
public void sort(int[] nums) {
    quicksort(nums, 0, nums.length - 1);
}

private void quicksort(int[] nums, int left, int right) {
    // 递归结束条件
    if (left < right) {
        // 返回的中枢点的位置
        int pivot = partition(nums, left, right);
        // 对中枢点左边进行排序
        quicksort(nums, left, pivot - 1);
        // 对中枢点右边进行排序
        quicksort(nums, pivot + 1, right);
    }
}

private int partition(int[] nums, int left, int right) {
    int pivot = left;
    // 设定最左边的为中枢点
    int pivotVal = nums[left];
    // 左哨兵的位置为left，右哨兵的位置为right。左哨兵表示这个位置的左边所有的值都小于pivotVal
    while (left < right) {
        // 要从右边哨兵开始找，寻找第一个小于pivotVal的，因为pivot右边都应该大于等于pivotVal（注意不是大于）
        while (left < right && nums[right] >= pivotVal) right--;
        // 寻找左边第一个大于pivotVal的
        while (left < right && nums[left] <= pivotVal) left++;
        // 交换左右哨兵
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
    // 左哨兵和右哨兵碰头，交换pivot与这个碰头的位置
    nums[pivot] = nums[left];
    nums[left] = pivotVal;
    // 返回新的pivot位置
    return left;
}

9.3 Stability & Algorithmic Bounds

Stability

排序算法的稳定性是指当一个待排序的序列中有多个相同的元素时，若经过排序这些元素的相对次序保持不变，则该算法是稳定的

insertion sort是稳定的，因为当下一个travelling item大于或等于前一个时，是不会进行交换的

quick sort不稳定

Alorithmic Bounds

所有排序算法的可能最优复杂度为$\Theta(NlogN)$

9.4 Radix Sort

不使用比较进行排序，即基数排序

LSD Radix Sort

Least Significant Digit Sort，从最小位开始的基数排序

首先找到整个数组中最大数的位数，假设为k，然后从个位到k位重复进行排序，如下所示：

假设有一串数值为

73, 22, 93, 43, 55, 14, 28, 65, 39, 81

首先根据个位数的数值将其分配到编号0-9的bucket中

将这些bucket中的数值进行收集

81, 22, 73, 93, 43, 14, 55, 65, 28, 39

再根据十位数的数值将其分配到编号0-9的bucket中

将这些bucket中的数值进行收集

14, 22, 28, 39, 43, 55, 65, 73, 81, 93

由于最高位为2，因此排序结束

复杂度为$O(kN)$，其中k为最大数的位数，N为数组个数

MSD Radix Sort

从最高位的基数开始进行排序，适用于位数比较高的情况

注意：和LSD不同，MSD在判断每一位的过程中需要将array拆分成多个sub array进行排序

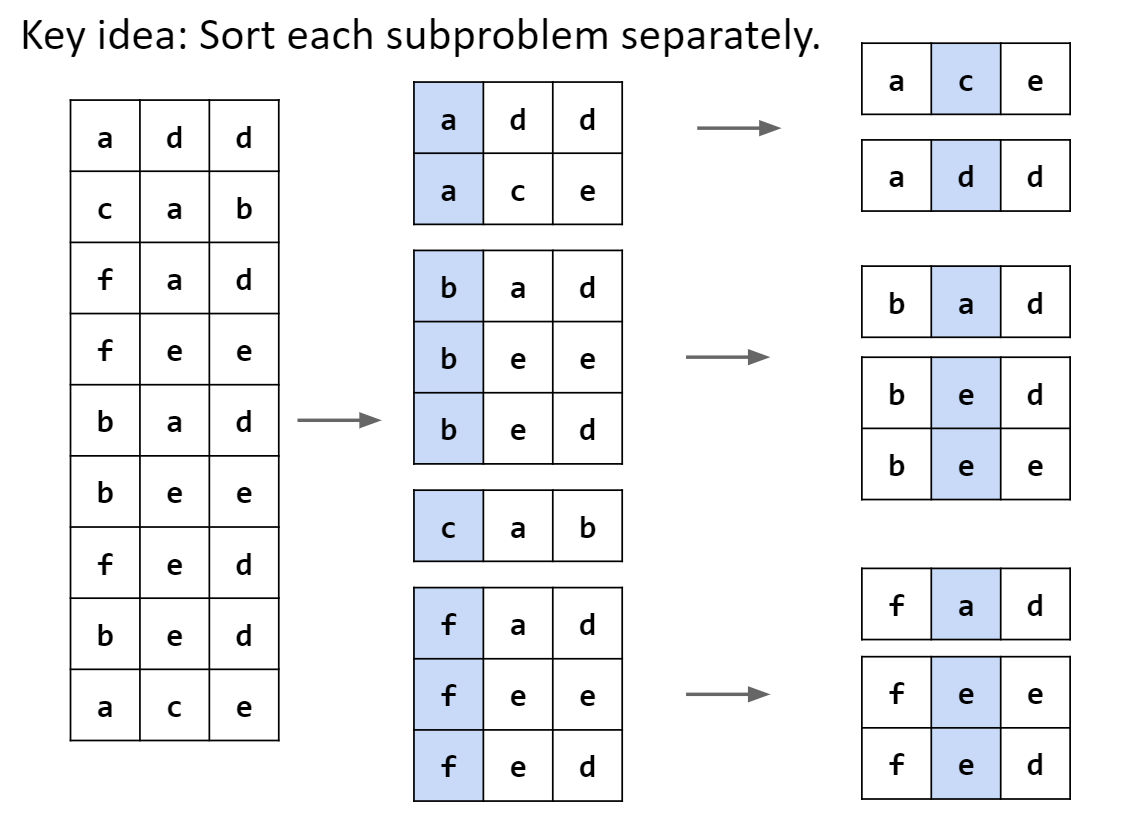
// radix sort
int len = nums.length;
int max = Arrays.stream(nums).max().getAsInt();
long exp = 1;
int[] buf = new int[len];
while (exp <= max) {
    // allocate 10 buckets, count each bucket's size
    int[] cnt = new int[10];
    for (int i = 0; i < len; i++) {
        int index = (nums[i] / (int) exp) % 10;
        cnt[index]++;
    }

    for (int i = 1; i < 10; i++) {
        cnt[i] += cnt[i - 1];
    }

    // put the original array into each bucket
    for (int i = len - 1; i >= 0; i--) {
        int index = (nums[i] / (int) exp) % 10;
        buf[--cnt[index]] = nums[i];
    }

    System.arraycopy(buf, 0, nums, 0, len);
    exp *= 10;
}

9.5 Tries

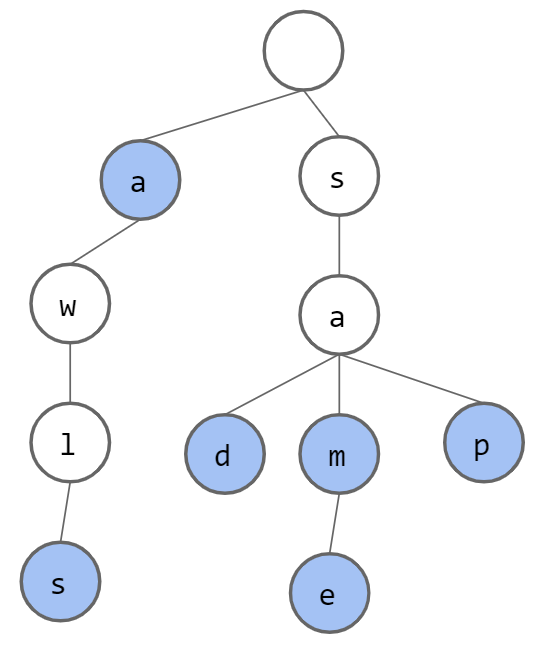
蓝色节点表示数组中有对应node结尾的元素，比如a、awals、sam、sad、sap、same

tries主要用在查找prefix上

trie implementation

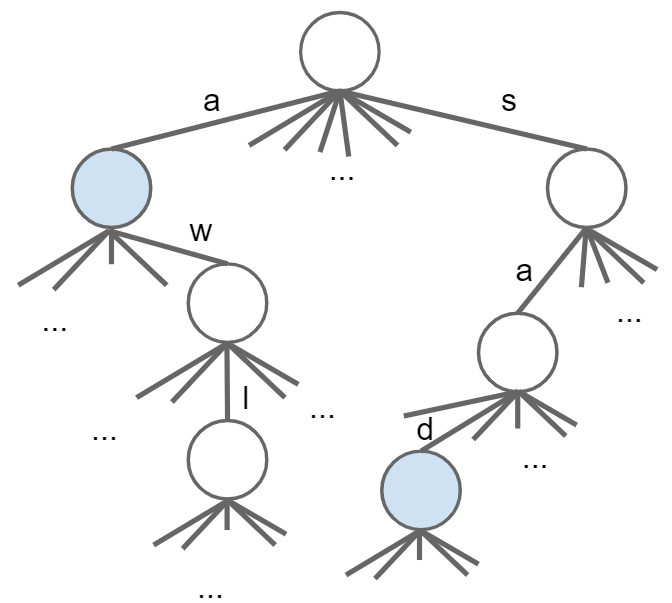
character不存储在node上，而是隐式地存储在link上，比如link[0]就是’a'

public class TrieSet {
    // support characters up through #128
    private static final int R = 128;
    
    private class Node {
        /* Up to R links */
        boolean exists;  // node is blue or white
        Node[] links;
        
        public Node() {
            links = new Node[R];
            exists = false;
        }
    }
    private Node root = new Node();
    
    public void put(String key) {
        put(root, key, 0);
    }
    
    private Node put(Node x, String key, int d) {
        if (x == null) {
            x = new Node();
        }
        
        if (d == key.length()) {
            x.exists = true;
            return x;
        }
        
        char c = key.charAt(d);
        x.links[c] = put(x.links[c], key, d + 1);
        return x;
    }
}

BinarayTrie的实现可以参考HW7

https://github.com/tommyfan34/cs61b/blob/main/hw7/BinaryTrie.java

UCB CS61B Lecture Notes

1 Introduction

1.1 Java Intro

1.2 JUnit

2 List

2.1 SLList (Singly Linked List)

2.2 DLList(Doubly-Linked List)

2.3 Generic List / Template

2.4 AList (Array List)

3 Inheritance

3.1 Intro and Interfaces

3.2 Overriding & Overloading

3.3 Inheritance

3.4 Static Type v.s. Dynamic Type

3.5 Higher Order Functions

3.6 Polymorphism

3.7 Abstract class

3.8 Prebuilt ADT

4 Java Syntax

4.1 Reference

4.2 Static

4.3 Autoboxing & Auto-unboxing

4.4 Immutability

4.5 Generic Method

4.6 Exception

4.7 Iterators

4.8 Access Control

5 Java Miscellaneous

5.1 Packages

5.2 JAR

5.3 Object Methods

6 Tree

6.1 Asymoptotic

6.2 Disjoint Sets

6.3 Binary Search Tree (BST)

6.4 Balanced BST

6.5 Advanced Trees

7 Hashing & Heap

7.1 HashTable

7.2 Priority Queue & heap

7.3 Data Structure Summary

8 Graphs

8.1 Intro to graphs

8.2 Graph Traversal

8.3 Shortest Paths

8.4 Spanning Tree

9 Sorting Algorithm

9.1 Basic Sorting Algorithms

9.2 Quick Sort

9.3 Stability & Algorithmic Bounds

9.4 Radix Sort

9.5 Tries